この研究はプランク以前にも多くの研究者が挑戦していました。しかし、どういうわけか温度と色の関係を1つの方程式で表現することが誰にもできなかったのです。
普通に考えると、実験結果から、温度(エネルギー量)と光の色(波長)の関係を書き出していき、この数字にあった方程式を作ればいいだけなのだから、意外と簡単にこの研究は完成しそうな気がします。
ところが、どの研究者が作った方程式も、なぜか答えが長波長(赤い光)になるほど実験結果とズレてしまったのです。
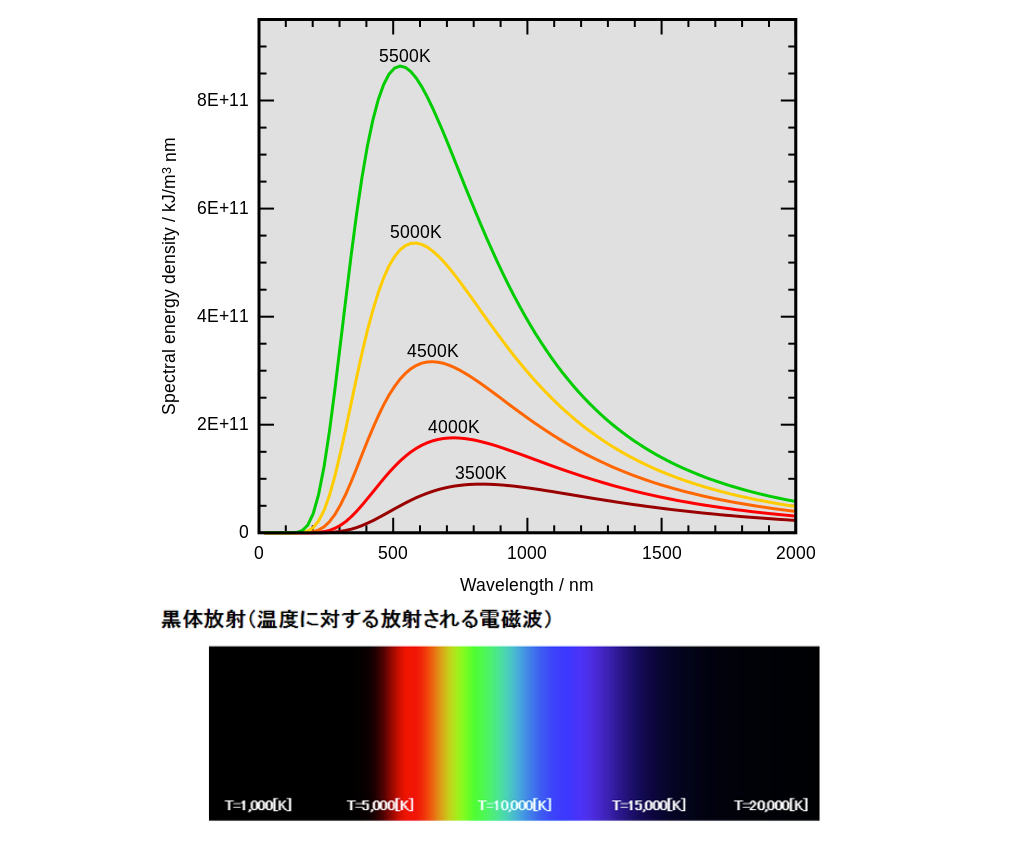
なぜ波長が伸びるほど、計算と実験結果はズレてしまうのでしょうか?
波長(波と波の間の幅)が短くなると、振動数(ある区間内で波打つ数)は増えることになります。実験結果と方程式のズレは、研究者たちの予想よりも振動数が大きいときにエネルギー量が大きくなってしまうことを意味していました。
そこでプランクは、もっとも単純な解決策として、振動数に定数を掛けるというアイデアを採用します。
光が1回振動するときに現れる最小エネルギー量を実験結果から導き出し、定数として方程式に組み込んだのです。
それが「E = hν」という数式です。
Eとは光のエネルギー量、ν(ギリシャ文字「ニュー」)は光の振動数を表します。そしてhとして導入されたのが、プランクが実験から導き出した最小のエネルギー量「プランク定数」です。
プランク定数hは6.626 × 10-34という恐ろしく小さい値で、日常的なスケールではまず気づくことのできないものです。







































