するとこの対峙関係もまた永遠に、つまり無限に続くことがわかります。
自然数組1人に対して偶数組が1人を常に出せる状況です。
別の言い方をすれば、自然数組が戦力を1ユニットだけ増やすと、偶数組も同じペースで戦力を1ユニット投じられる関係が永遠に続いていきます。
「だからなに?そんな当然のことを言って何になるのか?」と思うかもしれませんが、面白いのはここからです。
カントールは、この1対1の「フェアな出しっこ」が永遠に続けられる場合、それら2つの無限は等しいと考えました。
「いや、そうは言っても偶数のほうが伸びが早いし10個に5個しか出ないんだから、先に弾切れになるのでは?」と考える人もいるでしょう。
しかしそれもまた、有限の世界の常識です。
限りがない無限を扱う場合、お互いの端を比べることは基本的にはできません。
つまり弾切れを気にする必要がないのです。
そのため無限の比べっこを行うとすれば、存在しない端ではなく、フェアな対峙ができるかを気にするべきだとカントールは考えたわけです。
実際、自然数の対決相手に、奇数や2分の1ずつ増加する分数、0.3ずつ増加する小数、1ずつマイナスされていく負の数を対峙させても、同じような対峙関係が発生しました。
(※1、2、3……という並びと1億、2億、3億……という並びでもフェアな対峙が形成されます)
「〇〇ずつ増える」というルールを互いに守っている場合、互いに手札は無限なので「弾切れ」は起こらず永遠に1対1の対峙が実現するのです。
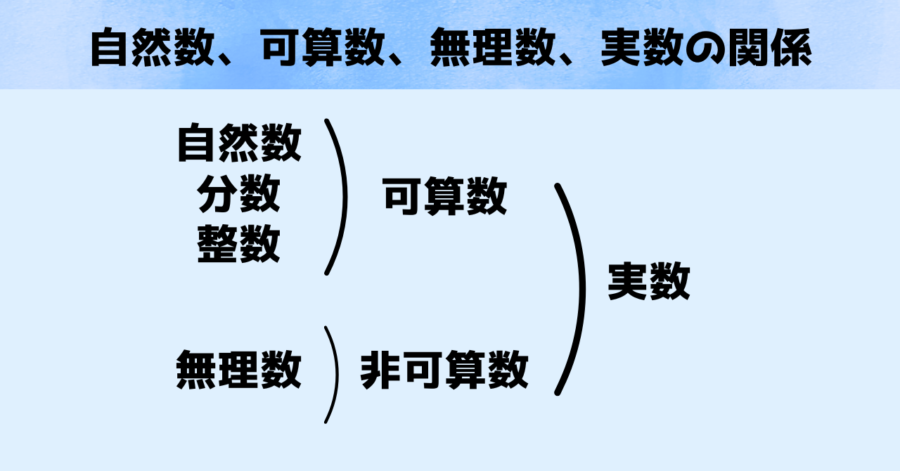
このことからカントールは自然数、整数、偶数、奇数、分数などの可算数と呼ばれる種類の数の無限はどれも同じ大きさだと結論しました。
そして可算無限の大きさをアレフ0(ℵ0)と定義し、無限というものを考えるときの基準点にしました。
また可算無限(ℵ0)よりも小さな無限をみつけることができないことから、可算無限(ℵ0)は最も小さな無限であると結論します。