しかし彼らと似た思想は2000年以上経過した現代では、かなり有力な説になっています。
今からおよそ150年前の19世紀、数学者のゲオルク・カントールによって無限には複数の種類があることがはじめて証明されました。

彼の証明はまず、数を線に沿って順に並べることからはじまりました。
まず1、2、3、4、5、6……という自然数を並べていきます。
自然数は人間が自然に数えられる最も単純な数の形で、指を折りながら1、2、3、4、5、6……と数えていける数のことを指します。
知っての通り、このようにして数えていける自然数は無限に存在します。
普通の人ならば、話しはここで終わってしまうでしょう。
それ以上考えることに意味などないし、考えたとしても何も結論など出そうもないからです。
しかしカントールは違いました。
カントールは自然数の次に偶数について考えます。
偶数は2、4、6、8、10……のように2で割り切れる数です。
そして偶数だけを線の上に並べても、その先は無限に続いていきます。
どちらも無限というわけです。
ですがカントールはここで「自然数の無限と偶数の無限を比べたら、どちらが多いか?」という無限の比べっこを思いつきました。
自然数も偶数も無限に続きますが、自然数が10個出現する間に偶数は5個しか出現しないのも事実です。
そうなると「自然数の無限は偶数の無限よりも2倍多く存在するのか?」という疑問が浮かびます。
もし数に果てがあるならば、その通りでしょう。
しかし無限が相手の場合は、単に2倍という話にはなりません。
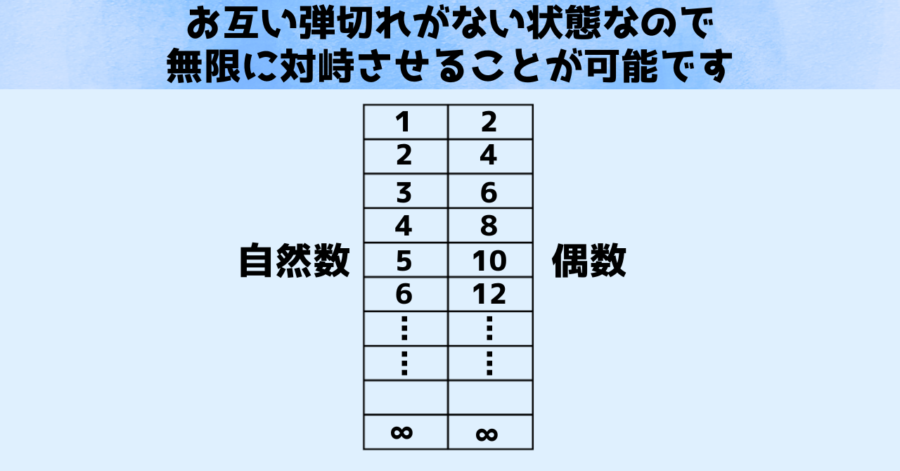
そこでカントールはより目に見える形で対峙を行うことにしました。
具体的には自然数の1に対して偶数の2を対峙させ、自然数の2には偶数の4を対峙させていきました。
自然数と偶数を構成する数たちに、スクラムを組むようにガッツリと対峙させてみたのです。