この\(y\)を新しく\(x\)として用いると、また新たな\(y\)を得ることができます。
これを繰り返すと、\(a\)が3以下の場合はある値に収束します。
\(a\)の値を3以上、そして段々と大きくして同じことをすると面白い現象が起こります。
下の図は、\(a\)(図中では\(r\))を変えたときに、操作の繰り返しによってどのような値(縦軸)に収束するかを示したグラフです。
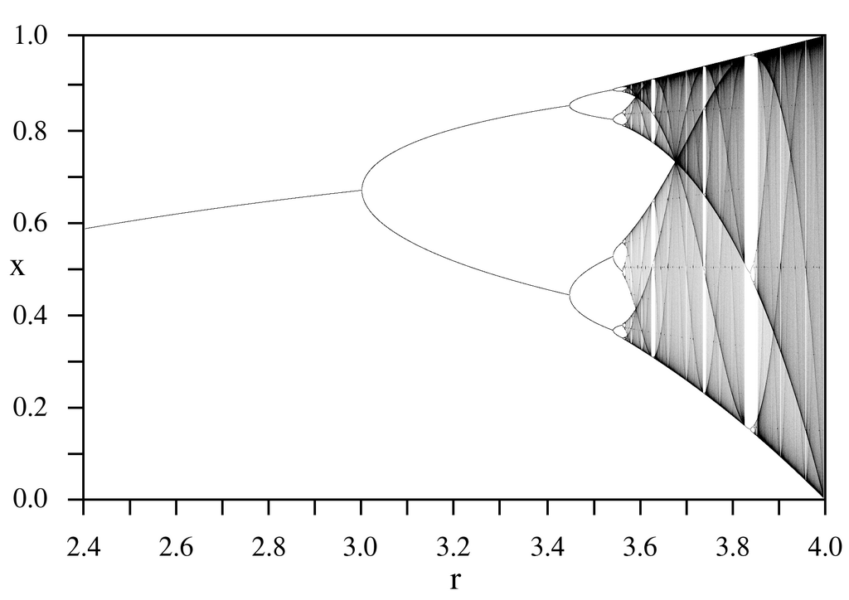
\(a\)が3を超えると、まず一つの値に収束しなくなり複数の値を交互に取るようになります。
そして\(a\)が3.56995を超えると\(y\)の最終的に取る値が極めて複雑になり規則性が見られなくなるのです。
この境界値3.56995はファイゲンバウム点と呼ばれています。
このように、カオス現象における予測できないというのはランダムであるという意味ではありません。
ロジスティック写像のように関係式は非常に単純でも、ある\(a\)における未来の\(y\)の値を書き表すことは非常に困難です。
この複雑さを指して、予測できないという表現をしているのです。
そうは言っても、近似値で良いから具体的な値が欲しいことも実用上はあります。
その場合はコンピュータによる数値解析が行われるのが一般的です。
しかし、今見たように\(a\)がファイゲンバウム点を超えたあとは\(a\)をごくわずかに変えただけでも未来の\(y\)の値には大きな変化が生じます。
そしてコンピュータといえども無限の桁数を扱えるわけではないため、真の値とは必然的に誤差が生まれます。
さらにその誤差は計算を繰り返せばどんどんと増幅されていきます。
その結果得られる値は、もはや真の値からはかけ離れたものになっているでしょう。
こうした理由により、予測は事実上不可能になるのです。














































