現在の天気予報では「アンサンブル(集団)予報」という手法を利用しています。
この手法では、まずある時刻に少しずつ異なる初期値を多数用意するなどして多数の予報を行います。
それらを用いて、平均やばらつきの程度といった統計的に情報を得ることにより気象現象の発生を確率的に捉えることが可能となります。
こうすることにより予測の信頼性を事前に推定できるようになりますし、複数のデータを用いることにより可能性のあるシナリオを複数予測することも可能になります。
現在は予報する期間や用途によって様々な予報システムを使い分けています。
下図は、2018年8月4日9時を初期値とした台風第13号の進路の5日予報です。
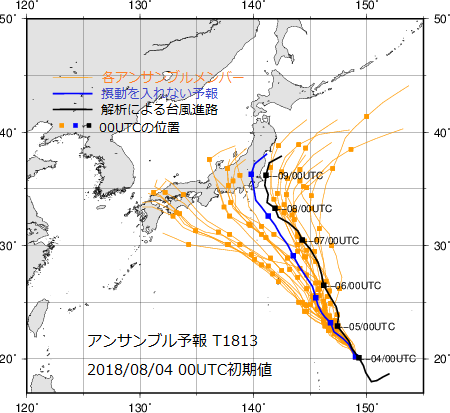
黒色の線が実際に台風が通った進路で、橙色の線は初期値を様々に変えて誤差を考慮した予測です。
また青色の線は初期値に含まれる誤差を考慮しなかった場合の予測となっています。
橙色の線と黒色の線を見比べると、実際の進路が予測のばらつきの範囲内に含まれていることがわかります。
初期状態のわずかな違いで時間とともに台風の取る可能性のある進路が広がっていきます。
しかし、これらのデータを複数集めて統計的に扱うことで、予測が当たる可能性を上げているのです。
パイを作るとカオスが現れる?
カオス現象に関連してもう一つ、パイこね変換(baker’s transform)というものを紹介します。
これはパイの生地の上に、何か意味のある絵や規則的な模様が描かれていたとして、パイを引き延ばして折り畳むという操作を繰り返したときにその絵がどの様に変化するか予想できるか? という問いかけが由来になっています。
やってみるとすぐわかることですが、ここにも複雑なカオス現象が潜んでいます。
パイこね変換を数学的な操作として簡単に表すと、次のようになります。










































