与えられた1✕1の正方形を横方向(x 方向)に2倍に伸ばし、縦方向(y 方向)に1/2に押しつぶす。
押し伸ばされた領域の内、元の1✕1の正方形の領域からはみ出た右半分の領域(1 < x ≤ 2 )を切り取り、はみ出ていない左半分の領域(0 < x ≤ 1 )の上に乗せる。
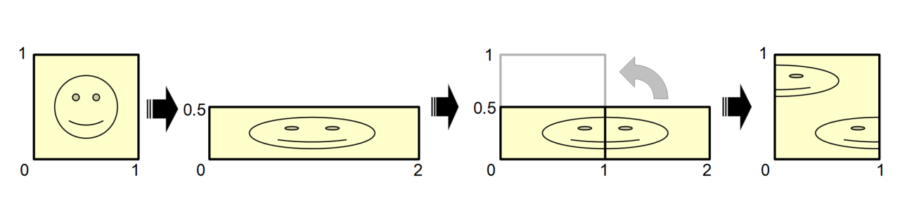
これを一回の操作とします。
1番目の操作は「引き延ばし」、2番目の操作は「折り畳み」に対応し、これらはカオス現象を発生させるための仕掛けとなります。
パイをこねつづけると、つまりこの変換を繰り返し行うとどのような変化が起きるのでしょうか。
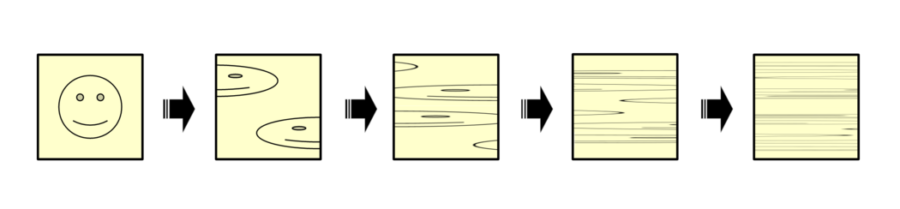
パイこね変換を4回繰り返すと、目印として付けておいた顔の形の面影はほとんどなくなり、混ざりあったような模様になってしまいます。
ここから更に変換を繰り返すと、より混ざり具合は高くなっていきます。
パイを小さな点の集まりとみなして考えると、初期の各点は離れ離れになっていき、初期に固まっていた領域は一様に全体へと広がっていきます。
この元々の秩序だった模様が変換によってどんどん無秩序になっていく様子は、カオスとしての性質を持っています。
パイこね変換によってある2つの初期点が離れていく度合いは指数関数的に変化するため、その未来の値は初期値の少しの変化によって大きく変わるのです。
この変換は料理のパイやうどんなどの生地を、押し潰しては折り畳むという作業を繰り返すことによって生地を材料の偏り無く一様にできることの説明とも言われます。
カオス現象は初期値に大きく左右され、ある程度時間が経った状態の予測は困難です。













































