逆に、上の図のように、コーヒーカップのカップ部分を平らにして、リング全体に均一になるよう捏ねていけばドーナツの形にすることができます。
このように伸び縮みする柔らかな素材を使うと、コーヒーカップとドーナツは1度もどこかを切り取ったり穴を開けたり、新たな接続部分を作らずに、滑らかに変形させていくだけで形状を行き来することが可能です。
この状態をトポロジー的には同じであると表現します。
このトポロジーの考え方を理解すると、「入口で片手を迷路の壁について歩き続ければいずれ出口にたどり着ける」という迷路攻略法がなぜ成立するのかという問題も解決できます。
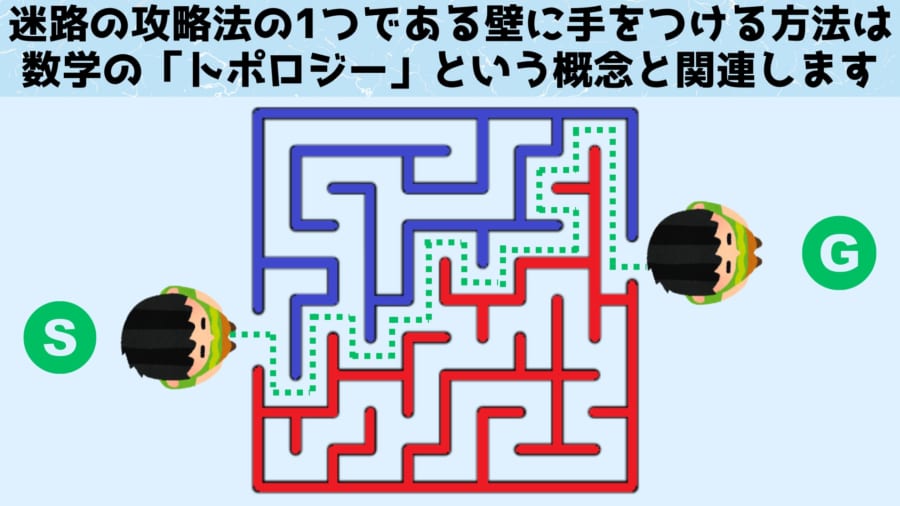
上の図は、スタートとゴールが端と端にある標準的な迷路を最短距離で攻略するルートを示しています。
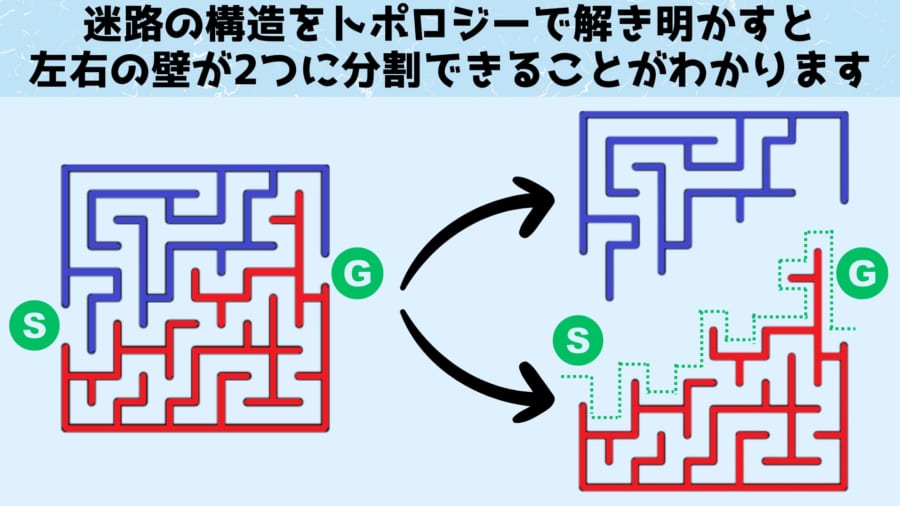
興味深いことに、迷路の左手側(青色)と右手側(赤色)を掴んで引っ張ると、この最短ルートは迷路を2分割する境目であることがわかります。
逆に言えば最短ルートとは、両側の壁の分割ラインだったと考えることもできます。
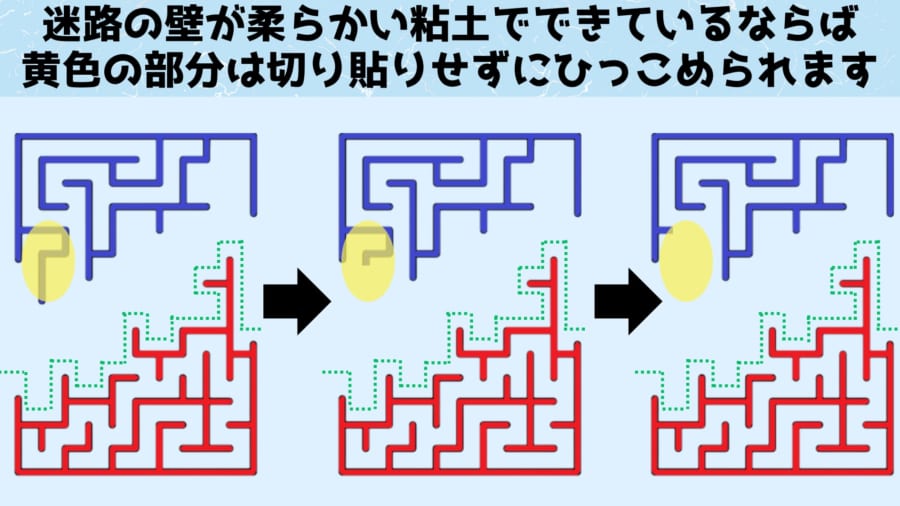
ここで先ほどのコーヒーカップとドーナッツの例のように、迷路の壁が柔らかい素材でできていると考えると、黄色で囲った「飛び出ている壁」を引っ込めても、トポロジー的には同じと言えます。
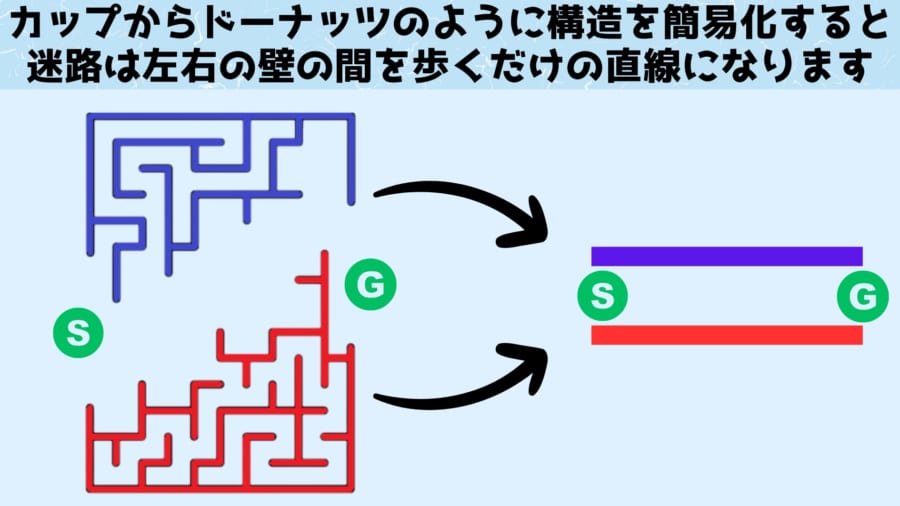
同様に飛び出ている壁を切り貼りせずにどんどんひっこめていくと、迷路は最終的に2つの壁に挟まれた直線ルートに変形させることができます。
この状態で「壁に手をあてる攻略法」を当てはめてみると、この攻略法とは、トポロジー的に同じという概念に基づいてゴールに向かっていることがわかります。














































