遊園地やゲームの中に登場する迷路は、人々を迷わし出口に到達するのを困難にします。
特に悪意を持って作られた迷路は、各地に同じようにみえる行き止まりや通路を持ち、私たちの記憶を混乱させてきます。
しかしどんな複雑な迷路であっても、必ず抜け出せる簡単な方法「手を壁に当てながら進む」という有名な方法が存在します。
この方法では左あるいは右手を壁にあてつつ壁に沿って進む方法です。
スタートとゴールが迷路の端と端に存在するパターンでは、まずこの方法で攻略可能です。
今回はこの「手を壁に当てながら進む」という方法が数学的にどのような意味を持ち、最終的に必勝法として機能するかを見ていきたいと思います。
といっても難しい数式などは出てこないので安心してください。
目次
- 迷路を数学的に解剖してみる
迷路を数学的に解剖してみる
迷路の攻略を数学者の視点から考える場合、必要となる考えは「柔らかい粘土で作られた素材を切り貼りしないで変形させる」という概念です。
この概念は「位相幾何学(トポロジー)」として知られています。
なにやら難しそうな呼び名ですが、言いたいことは単純です。
トポロジーでは物体を自由に変形できる粘土のように捉えています。そのため物体の形を区別する要素は、その物体に穴が空いているか? その穴はいくつあるか? という要素だけになります。
たとえば、トポロジーでは取っ手が一つだけついたコーヒーカップと、ドーナツは同じ種類の形として扱われます。これはどちらも穴が一つです。
イマイチ納得行かないという人は、粘土のドーナツをぐにゃぐにゃと変形させて、取っ手が一つのコーヒーカップを作ることを想像してみましょう。
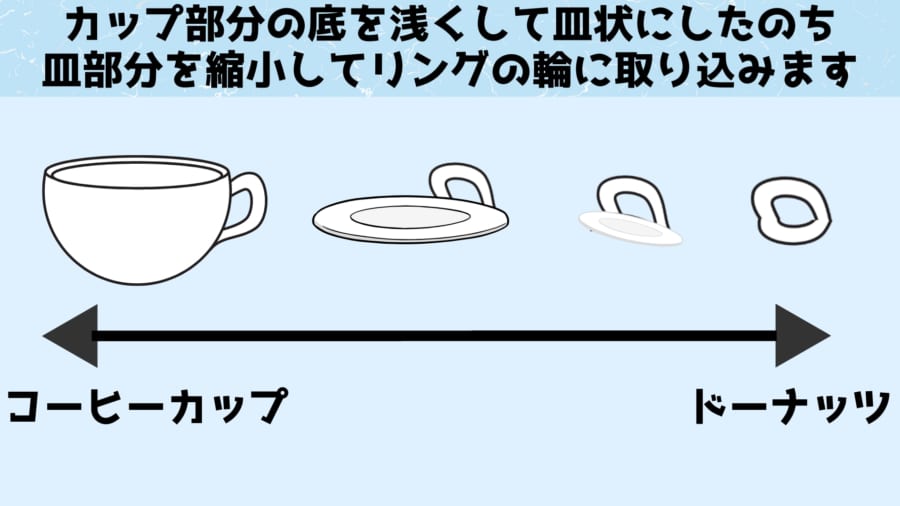
リングの一部分に粘土を集めつつカップを作れば、一度も粘土をちぎることなくドーナツからコーヒーカップを作れます。














































