といっても難しい話ではありません。
現在の宇宙論では、宇宙は時間の経過とともに加速度的な膨張を起こしていることが知られています。
この膨張の影響は超新星爆発や超大質量ブラックホール「クエーサー」から発せられる光にも影響を及ぼし、光の波長が空間と一緒に伸びていくことが知られています。
ゴム膜の上に波紋を描いたとき、ゴム膜を引っ張ると波紋の間隔が広がっていくのと同じです。
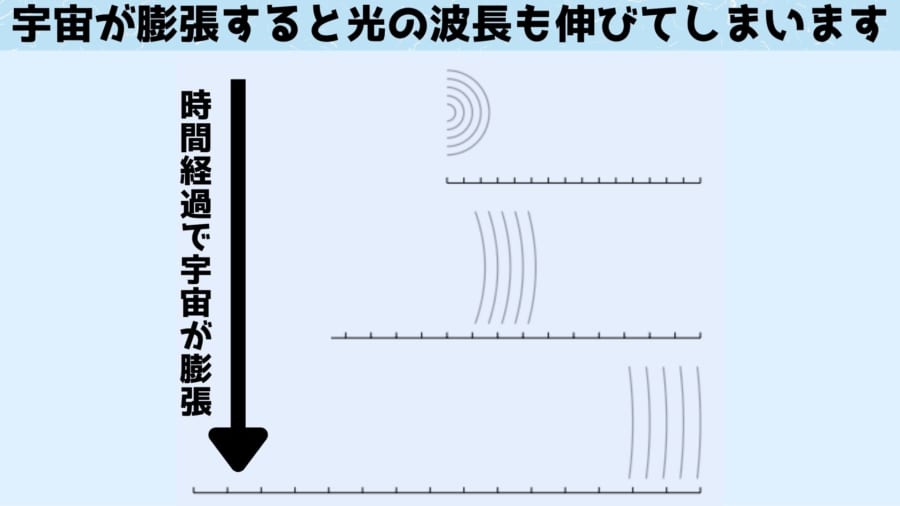
そのため発信源では波長が短い青の光でも、宇宙を旅して地球に到達するころには波長の長い赤い光に変化するという現象(赤方偏移)が起こります。
波長が伸びる度合いは、宇宙の膨張にどれだけ晒されたか、つまり古い時代に発せられた遠くの光ほど大きくなっています。
そのため波長が伸びる度合いを調べることで、光が発せられた時間を知ることが可能になります。
また光が発せられた時間に光の速度をかけ合わせて「速度×時間」をつくれば光の発信源までの「距離」も明らかになります。
小学校で習った「距離=速度×時間」の概念を使うわけです。
(※時速4キロで2時間走ったときの移動距離は「4×2」で8キロメートルになるのと同じです)

しかし先ほど述べたように現実の宇宙は常に膨張を続けており、宇宙を旅してきた光の距離は光の波長と一緒に自然に増加していきます。
すると宇宙の膨張につられて「距離=速度×時間」のうち、距離だけがドンドン勝手に伸びて行ってしまうことになります。
そのため左右をイコールで結び続けるには、速度か時間を増やさなければなりません。
普通に考えると時間の流れを変えるより、速度を変える方が合理的な印象を受けます
しかし実際の宇宙では、時間を一定に保つよりも光速を一定に保つ方が優先されます。













































