画像のような長方形のプラスチック板に穴が開いたタイプのスピログラフを見たことがある人は多いかもしれません。
他にも、主に子供用の玩具として複数の商品が販売されています。
このスピログラフが考案されたのは、1965年のことでした。
イギリス人発明家のデニス・フィッシャー氏は、1960年に自分の会社である「デニス・フィッシャー・エンジニアリング」を設立。
精密部品や様々なパターンの描写機械を製造する中で、スピログラフのアイデアを思いつきました。

そして考案から1年後にはライセンスを取得し、商品化。
瞬く間にブームとなり、1967年にはイギリスの「トイ・オブ・ザ・イヤー」に選ばれました。
1977年までには、3000万個以上のスピログラフが販売されており、現代でも「手軽に幾何学模様を描けるアイテム」として、人々の関心を引き付けています。
そんなスピログラフは、どのように美しい模様を描いているのでしょうか。もう少し詳しく考えてみましょう。
スピログラフはどうやって多様な幾何学模様をつくるのか?
スピログラフで描かれる曲線は、数学用語で「内トロコイド」と呼ばれます。
トロコイドとは、曲線の上を円が転がるときに、円の内部または外部の定点が描く曲線を指します。
円が転がる時、円周上にある点が描く曲線はサイクロイドと呼ばれ、こちらの方が有名ですが、トロコイドはサイクロイドの定点が円周上にないパターンを指しています。
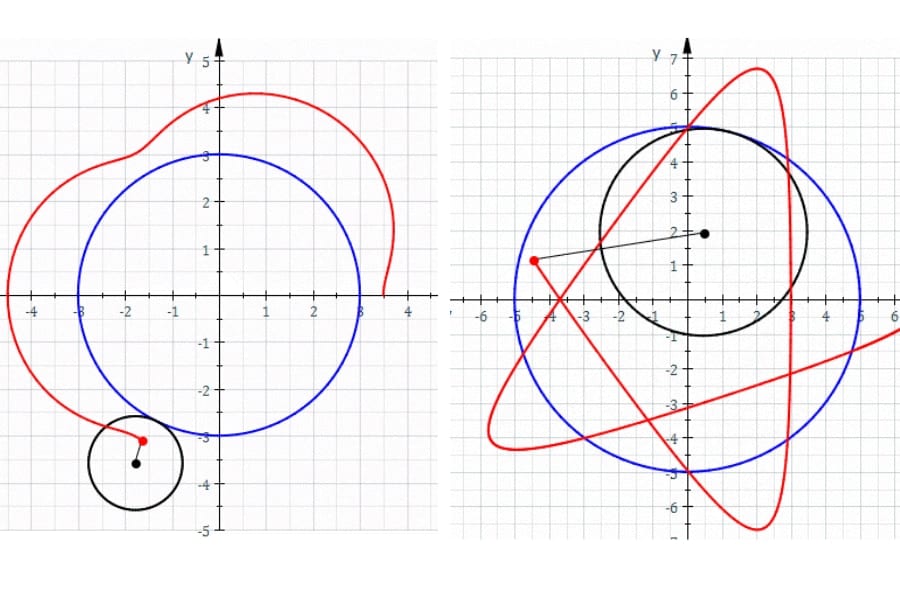
そして特に、円の転がる曲線も円形である場合、その定円の外側を動円が転がったケースを「外トロコイド」、内側を転がったケースを「内トロコイド」と言います。










































