本研究の“実験”は、理科室での化学実験のようなものではなく、コンピュータ上と理論上の仮想工作室での検証に近いイメージです。
研究者たちは、正三角形と正方形が「3ピース以下の切り分けを共用できるか」を洗い出し、候補を紙上でも再現しながら「果たして正方形を組み立てられるか」を確かめました。
最初は試行錯誤の連続で、多くのパターンが失敗に終わったそうですが、その後「マッチングダイアグラム(matching diagram)」という手法が開発され、大きく進展したといいます。
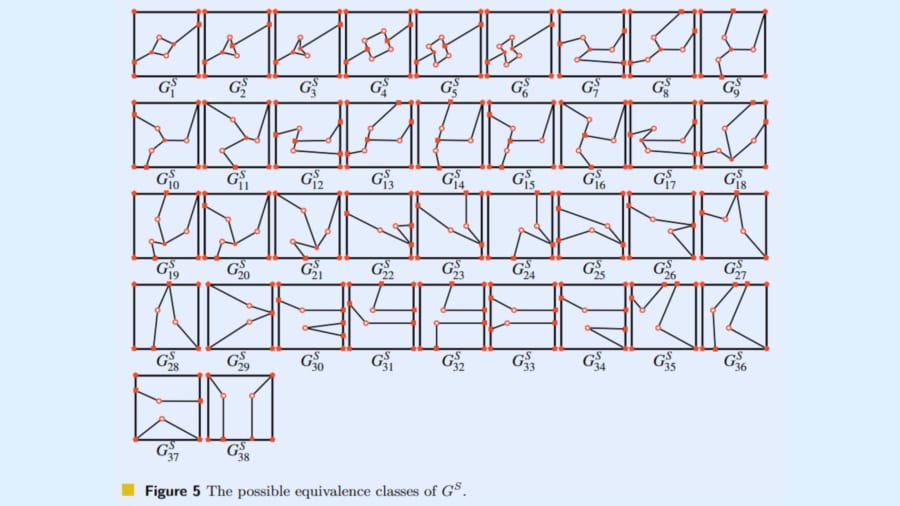
これは、切り分けられたピースの“頂点”や“辺”をグラフ理論を使って対応付けし、「このピースのどの辺が三角形のどこに対応し、正方形を組むときにはどこへ行くか」を可視化するものです。
まるでジグソーパズルのあらゆるピースを片っ端から当てはめてみて、合わない組み合わせを次々に“潰して”いくようなイメージで、非常に地道ながら“切り分けと再配置”を厳密に追跡できるという点が特徴的です。
その結果、研究チームは「3ピース以下で正三角形を正方形にする切り方は存在しない」ことを明確に示すことに成功しました。
論文著者の1人である上原教授も「1世紀以上を経て、正三角形と正方形には3つ以下の多角形ピースでは共通の分割がないことを証明し、ついにデュードニーのパズルを解きました」と述べています。
さらに、この手法は単に「最小ピース数」の答えを示すだけでなく、ほかの図形同士の分割問題にも応用可能という道を拓いた点で画期的といえます。
今後、最適な形状切り出しを求められる製造プロセスや繊維デザインなど、さまざまな分野での活用も期待されるでしょう。
3ピース以下は不可能、でもここからが始まり――進化する分割の最前線