ところがパラ粒子は「ある定員数まではOK、しかしそれを超えると一切入り込めなくなる」という、中間的なルールを持つと考えられているのです。
もし本当にこの性質が存在し、しかも観測可能な形で実現するならば、「1人きりか、または大勢か」という二択しかなかった世界に新たな選択肢が加わることになり、量子力学は大きな変革の時が訪れるでしょう。
次はパラ粒子を見つけるためにつかった数学的なテクニックを言語化して紹介していきます。
数学の力で「ありえない粒子」をあぶり出す
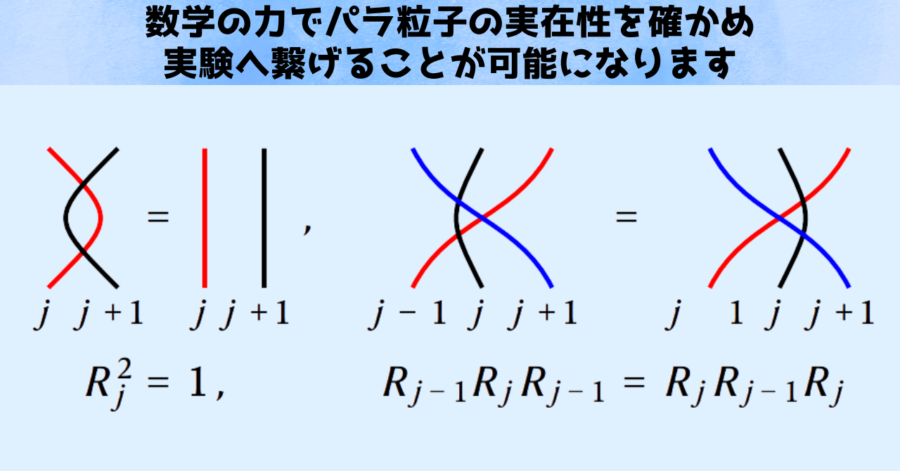
観測が困難だったパラ粒子をどうやってあぶり出すのか?
研究チームはまず理論の組み立てからはじめ、従来の考えにアインシュタインの理論を組み込み、光より速い情報伝達が起きないことや、時間変化が破たんしないこと(ユニタリティー)といった原則を守りながら、パラ粒子を「自由粒子」という扱いやすい形に整理しました。
これまで「どうせ観測できない」と思われていたパラ粒子を、実際に物質の中で“集団の振る舞い(準粒子)”として観測できる場合、どんなものになるかシナリオを描いたのです。
さらに、研究者たちは量子スピンモデルというシンプルな理論空間を用意し、シナリオ通りにパラ粒子が振る舞うかを検証しました。
具体的には1次元や2次元のスピン鎖(たとえば、整然と並んだコマのようなものをイメージしてください)をコンピュータで再現し、その中でパラ粒子らしい交換統計が自発的に生まれる様子を検証しました。
そして大事なのは、これらがただの数式上のお話ではなく、実験によって検証できる形でデザインされていることです。
もし特定の材料や測定技術をそろえれば、スピン系のエネルギーの模様(励起スペクトル)や衝突実験(散乱)を通じてパラ粒子の足跡を追えるかもしれないといいます。














































