ケインズモデルの投入
さて、高田がライバル視していた同世代のケインズの最単純モデル(ケインズ、1936=2012:118)では、国民総生産=国民総所得=消費+投資、すなわち
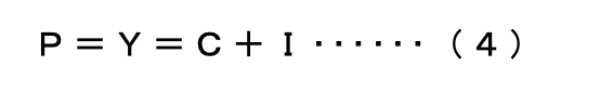
となる。そこでは「国民総生産」(P)は「国民総所得」(Y)と等しく、「消費」(C)と「投資」(I)の合計で得られる。だから、一般論としても社会システム全体での「所得」を増やすには「消費」と「投資」を増加させるしかない。もちろんそこにはさまざまな制約がある。
たとえば「投資が貯蓄のすべてを吸収し得なくなる」(高田、1955:14)とみたうえで、高田は投資を「産業投資と公共投資の両者を含む」(同上:15)とした。私も実感的にはこちらを支持する。
そうすると、ここでも投資(I)を産業投資(II)と公共投資(Ip)とに二分割して、
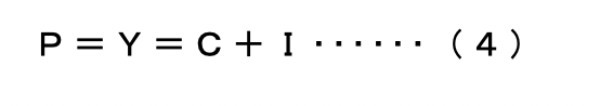
を得る。
この基本的な立場は「人口の増加は需要の増加を意味し、資本の増加は供給の増加を意味する」(高田、1932:110)のなかで、供給が需要を創り出すという古典派経済学と需要に合わせて供給がなされるとしたケインズ学派との両者間の対立を論じつつも、「需要が供給を決定する」という流れに合致する。ただし、この認識からすると、人口減少は「需要の減少」を意味し、需要が減れば資本にとっては売り上げが落ちることになり、「供給の減少」に直面してしまう注16)。
ただし、高田(1955)では、投資は「多義的」であり、ケインズの乗数理論は「公共投資」のみに当てはまり、「産業投資」には期待しがたいとした(同上:145)。果たしてそうか。
高田とケインズの組み合わせ
ここで、高田人口方程式「SB=dP」に、ケインズの最単純モデル「Y=C+I」を組み合わせると何が見えてくるかという思考実験をしてみよう。厳密な数学モデルとは言えないかもしれないが、高田の生産力Pとケインズの国民総生産(国民総需要)Yとは等しいとして、「P=Y」と仮定すると、(1)から
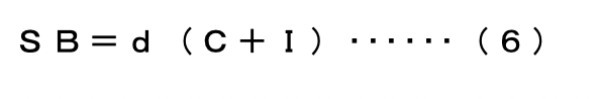
ができる。(5)を使うと
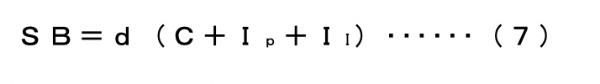
が得られる。さらに
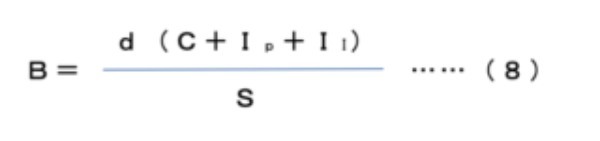
となる。これは(2)と全く同じである。
そこで(8)を文章で表現すると、「人口数=分配係数×国民生産(産業投資+公共投資)÷生活標準」となる。
人口数はこのような方程式で得られるのだとすると、人口増加とは、右辺の分子を大きくするか、分母を小さくするか、この両方を同時に行うかしかない。
このうち、分母を小さくすることは、生活水準とりわけ消費を落すことと同義だから、国民の大半は賛成しない。したがって、人口増加には分子を大きくし続けるしかない。すなわち、政府が公共投資、産業投資、消費のいずれかもしくは全てを拡充する政策に収斂する。









































