そんな中、英国の歯科医、ロリー・マクスウィーニー氏が注目したのは、ダ・ヴィンチが残した手書きのメモでした。
そこにはこう書かれていたのです。
「脚を開いたとき、その空間は正三角形となる」
この「正三角形」こそが、ダ・ヴィンチの幾何学の秘密を解く鍵でした。
そしてマクスウィーニー氏は、この三角形が1864年に歯科医ボンウィルが提唱した「ボンウィルの三角形」とほぼ一致することを見出します。
ボンウィルの三角形とは、歯科解剖学のなかで知られ、下あごの左右の関節と前歯の中心を結ぶ三角形のことで、理想的な咬み合わせやあごの動きの設計に使われています。
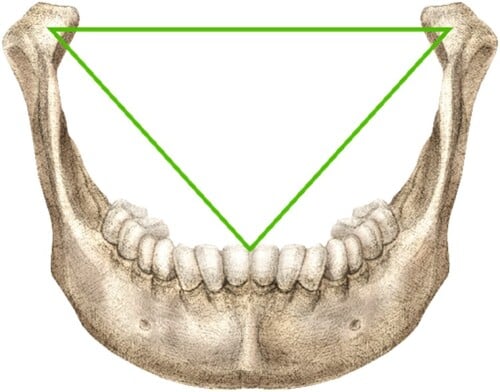
驚くべきことに、この三角形を元に図を構成すると、ウィトルウィウス的人体図に見られる正方形の一辺と円の半径の比率が1.64〜1.65となったのです。
これは自然界で効率的な構造の設計に広く見られる特別な比率「1.633」に非常に近い数値でした。
では「1.633」は自然界においてどれほど重要な数値なのでしょうか?
自然界の最適な設計原理
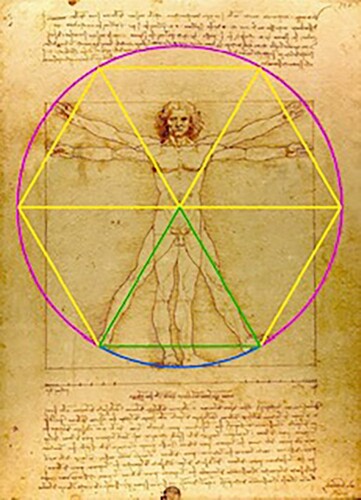
この「1.633」という比率、実は単なる数字ではありません。
それは原子の結晶構造や球体を最も効率的に積み重ねる方法、さらには自然界における“最適な空間の使い方”に共通して現れる数値なのです。
歯科の世界では、あごの骨がこの比率に沿った構造を自然に形成しており、理想的な歯の噛み合わせや顎の運動に必要な構造を示した「モンソンの球」や「咬合理論」などの分野でもこの数字が登場します。
また現代の研究では、人間の最適な頭蓋骨の構造にもこの比率(1.64±0.04)が存在することが確認されており、これは人類に特有の現象だと考えられています。







































