カラビ・ヤウ多様体は特殊な幾何学的性質を備えた空間構造で、複素3次元（実6次元）の“ドーナツ”をさらに複雑にしたようなイメージがしばしば用いられます。
弦理論はこうした追加次元や超対称性などを仮定する一方、直接的な実験証拠に乏しいため、「検証が難しい理論」として批判も受けてきました。
しかし今回のブラックホール散乱研究において、弦理論の核心部分と考えられる数学的エッセンスが重力波現象と直接結びついた可能性が示唆されたのです。
ある意味では、観測が難しいといわれてきた弦理論の要素を、ブラックホールという宇宙最大級の“実験場”で垣間見ることに成功した格好です。
ブラックホールを素粒子と考えると弦理論が見えてくる
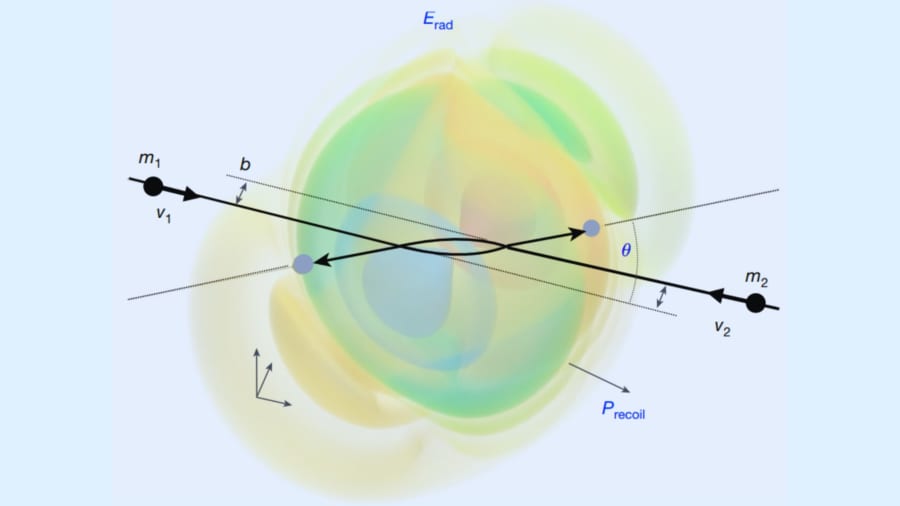観測不能と言われた弦理論を宇宙実験場へ / 宇宙という巨大なビリヤード台で二つの超重量キューボールがニアミスする“スローモーション映像”だと想像してください。左上から突進するブラックホール m₁ と右下から逆方向に飛ぶ m₂ は、ギリギリ衝突を避けつつ互いの重力で強烈にカーブをかけ合い、最接近点 b を境に方向を急旋回します。このとき二つの天体は、まるで池に石を落とした瞬間のように時空へ波紋——重力波——を一気に放ち、図の中央ではその波紋が虹色の渦となって描かれています。赤やオレンジの濃い色は「ここで大量のエネルギーが放射された」ホットスポットを示し、外側へ行くほど色が薄まり波が弱まっていく様子が読み取れます。急ブレーキを踏んだ車が反動で跳ね返るように、重力波を吐き出した反作用で m₂ は図中の矢印方向へスピンアウトし、これがリコイル（蹴り返し）速度です。/Credit:Mathias Driesse et al . Nature (2025)
では、研究チームはどのようにしてブラックホール散乱から弦理論由来の数学構造を見いだす方法を発見したのでしょうか？
鍵となったのは、素粒子物理で培われた散乱計算の手法をブラックホール研究に応用するというアイデアです。
