実際、LIGOやKAGRAなどの現行重力波望遠鏡は今後さらなる高感度化が予定されており、2030年代には欧州の地下観測所アインシュタイン望遠鏡や米国のCosmic Explorer、さらに宇宙重力波アンテナLISAといった次世代計画もスタートする見込みです。
これらの施設が稼働すれば、ブラックホールが合体せず高速ですれ違う散乱イベントによる重力波を初めて検出できる可能性が高いです。
このときに備え、理論面でも散乱イベントの波形を高精度に予測し、「どんな信号を探せばよいか」のテンプレートを準備することが求められています。
今回の研究はまさにこの課題に取り組んだものです。
弦理論は宇宙のあらゆる素粒子や力を一次元の「ひも」の振動モードで説明しようとする仮説であり、典型的には（時間1＋空間9）＝10次元を想定します。
目に見えない余剰の空間次元は極めて微小に折り畳まれて存在すると考えられ、その有力な折り畳み方がカラビ・ヤウ多様体です。
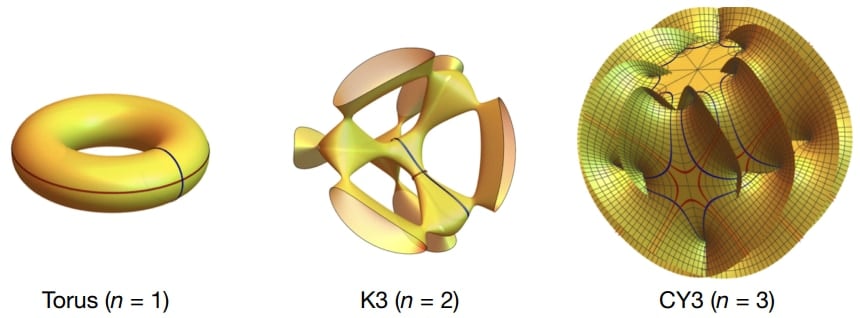ブラックホールを素粒子と考えると弦理論が見えてくる / 図は、ブラックホール散乱の方程式の背後にひそむ “見えない空間のかたち” を一枚で示したコンセプト図です。左から順に、一次元トーラス（ドーナツ形）に対応する楕円曲線、その二次元版であるK3 曲面、そして六次元のカラビ-ヤウ三重多様体（CY3）を、私たちが 2D で眺められるように投影して並べています。 トーラスは「ドーナツを一周する二種類の輪」を赤と青で描いたシンプルな形ですが、右へ進むにつれ表面が複雑に折り紙のようにねじれ、CY3 では六次元の“超ドーナツ”が絡み合ったようなシルエットになります。これら赤・青の輪は、それぞれの多様体の基本サイクル（Γₙ）を表し、その輪に沿って n 形式 Ωₙ(x) を積分すると“周期”と呼ばれる値が得られます。周期はブラックホール散乱の高次計算に登場する特殊関数そのもので、たとえば CY3 の周期は放出エネルギーや反動速度の数式に直接入り込みます。/Credit:Mathias Driesse et al . Nature (2025)
