例えば3次方程式の解はカルダノの公式は上の図に示したように、かなり複雑な形で示されています。
4次方程式にもフェラーリの解法があり、一般的な代数的解は存在しますが、式の複雑さはさらに増します。
2~4次の公式はいずれもルートの存在を前提としています。
なので多くの人々は、何乗しようとそれに合わせてルートのレベルを上げていけば対応できると思いがちです。
しかし不思議なことに5次方程式は4次以下と同じように、ルートを使って表すことができません。
5次方程式の解を導くにはより高度な特殊関数が必要不可欠になるのです。
ルートは2~4次方程式ではXの値を綺麗に解きほぐす包丁となれても、5次ではいくら重ねても解けない最後の1塊のようなものが残ってしまうのです。
多くの人は「えっ、なぜそこから先が急に不可能なの?」と感じるでしょう。
3次や4次の公式があまりに複雑なため、「こんなに複雑なら5次だって理屈の上で頑張ればできるのでは?」という直感が働くかもしれません。
しかしガロア理論では、5次以上の方程式の構造は「根号の繰り返し」でほどけるものとはまったく別次元であると厳密に示されるのです。
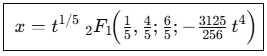
まさにここに不思議な断絶があり、数学史の大きな壁としてあらゆる研究者を阻んできました。
ところが今回研究者たちは、この「5次以上は不可能」という伝統的定説に対し、根号ではなく数列や図形的な概念を使うことで4次と5次を飛び越えられる「一般的な解」を形式的に導こうとする新アプローチに挑みました。
図形と数列で5次方程式の解を作る

新しいアプローチのキーポイントは、「組み合わせの数を数える特殊な数列」を活用することです。
まず、たとえば「カタラン数」と呼ばれる有名な数列があります。






































