アリスタルコスはアナクサゴラスの考える通り、月が太陽光を反射しているなら、半月のとき月と太陽と地球は直角三角形を描いているはずだと考えました。
もしそうなら、地球と太陽の作る角度がわかれば、三角法によって月と地球の距離と地球と太陽の距離の比を明らかにすることができます。
アリスタルコスが実際に半月のとき、太陽と地球が作る角度を測定したところ、それは87°でした。このことからアリスタルコスは、太陽までの距離は、月までの距離のおよそ20倍だと導きました。
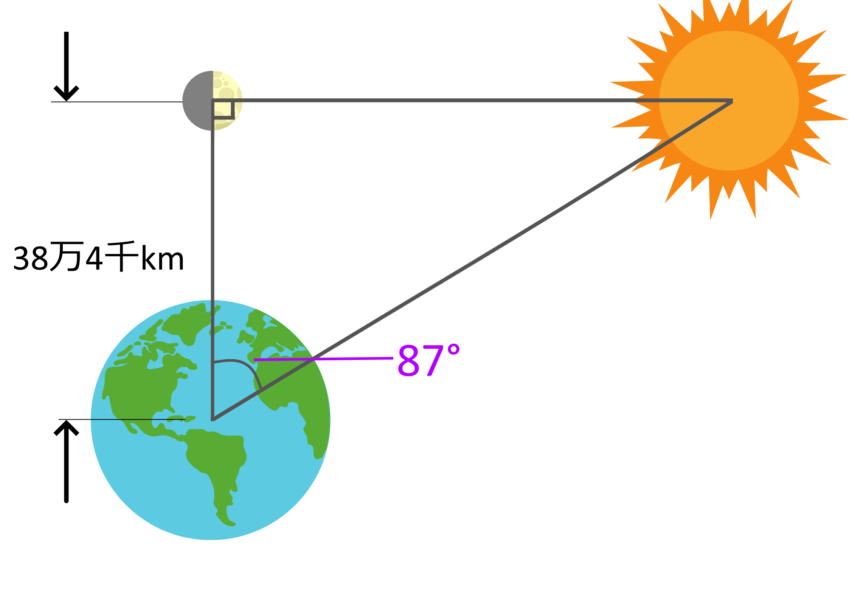
実際は、現代の技術で調べると、この角度は正確には89.85°であることがわかっており、太陽までの距離は月までの距離のおよそ400倍です。
アリスタルコスは、この角度を調べるためにかなりの苦労をしたでしょうが、技術的な精度の限界で正しい値を知ることはできませんでした。
しかし考え方は間違っておらず、ズレがあるものの彼は地球と太陽の距離を推定することができたのです。
では、最後に太陽の大きさはどれほどなのでしょう?
この測定方法はすでに解説しています。
日食のとき、月は太陽をすっぽりと覆い隠してしまいます。このことからアリスタルコスは、地球から見た月と太陽の大きさがほぼ同じであることを知っていました。
だとすれば、さきほど爪と月を使って比を取った方法を、今度は月と太陽で行えばいいのです。
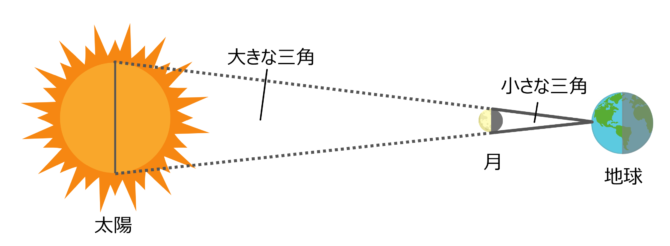
月の大きさと、月までの距離、太陽までの距離はわかっているのですから、
【太陽の大きさ:月の大きさ = 太陽までの距離:月までの距離】
という関係を利用して、おおよその太陽までの距離を知ることができるのです。