満月の夜に、月に向かって腕を伸ばし、人差し指を立てると指先の爪がすっぽりと月を隠してしまいます。このとき指先の爪と、月の大きさはほぼ同じに見えることになります。
これは、爪の大きさと腕の長さの比が、月の大きさと月までの距離の比に等しくなっていると考えることができるのです。
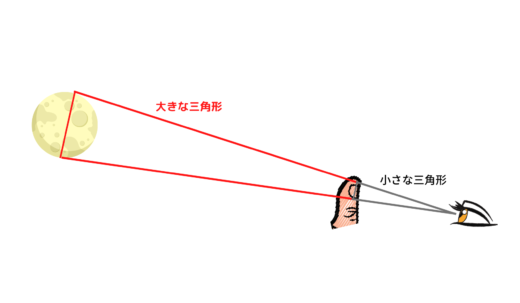
実際はもう少しきちんとした道具を使用して測ったでしょうが、エラトステネスがこうした方法で比率を計算したところ、月までの距離は月の大きさのだいたい120倍だろうと検討がつけられました。
つまり月の直径の120倍、約38万4千キロメートルが地球から月までの距離だとわかったのです。
では、月よりもはるかに遠く、はるかに巨大な太陽を古代ギリシャ人はいかにして測定したのでしょうか?
月を利用した太陽の測定
宇宙の神秘に近づくために、まず人類に必要だったことは、太陽や月が神の化身ではなく、宇宙に浮かぶ天体であると理解することでした。
このことを最初に主張したのは、紀元前400年代の哲学者アナクサゴラスです。

アナクサゴラスは、太陽を神などではなく白く熱い岩石であると主張しました。夜空の星も同様の熱い岩石だが、こちらは非常に遠くにあるので太陽のようには感じられないのだと言ったのです。
さらに月は冷たい岩石であり、太陽の光を反射しているだけだと論じました。
彼の住んでいたアテナイは、かなり学問に寛容な都市でしたが、さすがに太陽や月を神ではなく岩石だ、と主張したことには反発が多く、残念なことに彼は街を離れることになってしまいます。
そんなアナクサゴラスの考えを後に発展させたのが、さきほど月の大きさの測り方でも登場したアリスタルコスです。














































