その秘密の1つは、この三角形の形状にあります。
三角形なのに常に同じ幅で転がる「ルーローの三角形」
ここで利用されている理論が「ルーローの三角形」と呼ばる、正三角形の各辺を膨らませたような形状です。
(「ルーローの三角形」は曲線を持つため、正確には三角形ではありません。この記事では「ルーローの三角形」という名称から、ゴルディエフ氏が開発した自転車を「三角形自転車」と呼称します)
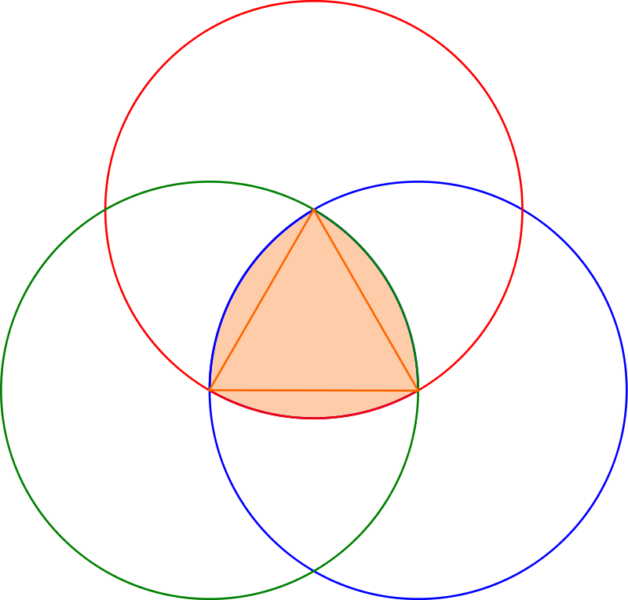
ルーローの三角形は、このように各頂点からコンパスで円を描くことで簡単に作ることが出来る図形です。
そしてこのようにして描かれたルーローの三角形は、転がしたときに常に幅が一定を保つ定幅図形と呼ばれる図形になるのです。
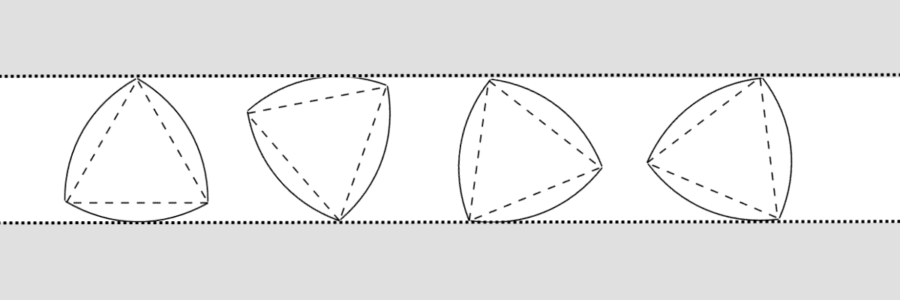
ただし、下の動画を見ると分かりますが、ルーローの三角形は高さが一定のまま転がることができますが、その際の重心(中心点)の位置は一定ではなくなります。
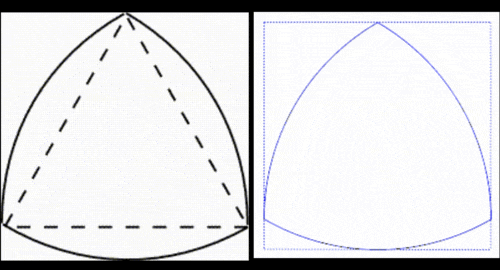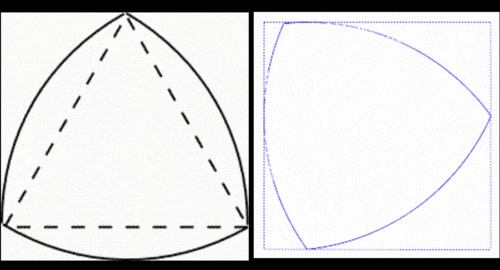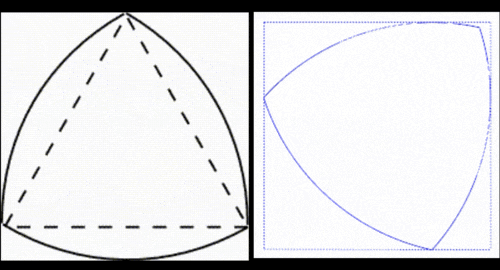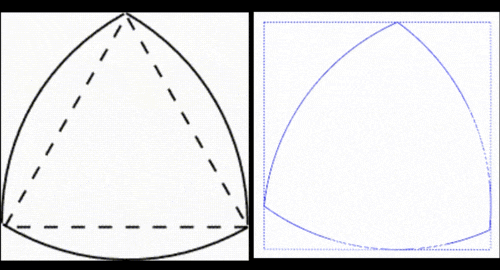
このため、単純に自転車の車輪をルーローの三角形に置き換えたとしても前進する度に車体ごと上下に動いてしまうのスムーズに移動することはできません。
そこでゴルディエフ氏は、車輪の上部が常に一定の高さを保つように押さえつける地面と平行なローラーを追加しました。
また各車輪の中心軸の部分を可動式にして、上下の動き(衝撃)を吸収できるようにしました。














































