前述のようにメビウスの輪は小学生にも簡単に作ることができますが、材料として渡される帯の形状によっては、かなりの困難が生じます。
たとえばアスペクト比1の正方形の折り紙でメビウスの輪を作ろうとしても、紙同士がぐちゃぐちゃに接してしまって(帯が帯に食い込んで)、綺麗なループ状になってくれません。
「綺麗なメビウスの輪を作るのに必要な最低限のアスペクト比はどれくらいか?」
この質問は単純に思えますが、実はメビウスの輪が最初に発見された1858年から現在に至るまで、誰も答えを数学的に証明することはできませんでした。
メビウスの輪を切り開く
綺麗なメビウスの輪を作るに、材料の帯に求められる最低限のアスペクト比はどれくらいか?
50年以上にわたる謎を解明するため、ブラウン大学の数学者シュワルツ氏はまず、メビウスの輪に顔を近づけてみました。
この稜線は完全な直線であり、メビウスの輪が始まって終わる境界線、つまり材料となる帯の端と端になりえる部分です。
小学生の工作では端と端をくっつけるときに「のりしろ」部分ができてしまいますが、この稜線部分は一切の遊びを許さない、始点と終点が同じ境界線となっています。
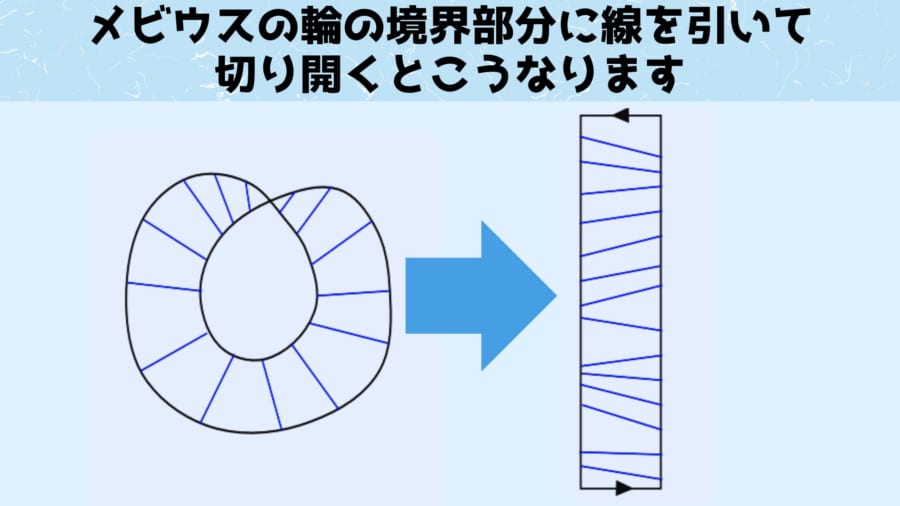
シュワルツ氏は、このような稜線が発生する境界線部分に、上の図のように、青い線を引いていきました。
そして帯の横幅(全長)を短くした場合に、境界線がどのように変化していくかを数学的に分析しました。
結果、最も短いメビウスの輪を切り開くと展開図は台形になり、材料として求められる帯のアスペクト比は「√3」になることがわかりました。
私たち人間は四角形、長方形、帯を直感的に分類しています。
そのためある人にとってはアスペクト比5:1が長方形という2次元的な認識であっても、別の人にとっては帯として、やや一次元的(線)な要素の強い認識をされてしまいます。










































