■「0で割ると0になる」と覚えると悪影響が…
こちらの疑問に対し、森山氏は「すぐに思いつく弊害としては、小学算数や中1数学で学習する『反比例』の指導です」と例を挙げる。
同単元では「y=(決まった数)÷x」という関係が成り立つとき、「yはxに反比例する」と呼ぶことを小6算数で学習し、小6時点ではxは正の数の範囲、中1になるとxは負の数の範囲まで含めて学習する。
さて、ここで一度「y=6÷x」のグラフを見てみよう。
小6で学習するのはグラフの右上範囲だけだが、中1になると図のグラフ全体を学習する。同グラフは「y=6÷x」という関係式を成り立たせるようなxの値をyの値をペアにして点を無数に打っていった結果、滑らかな曲線が描かれる…というもの。
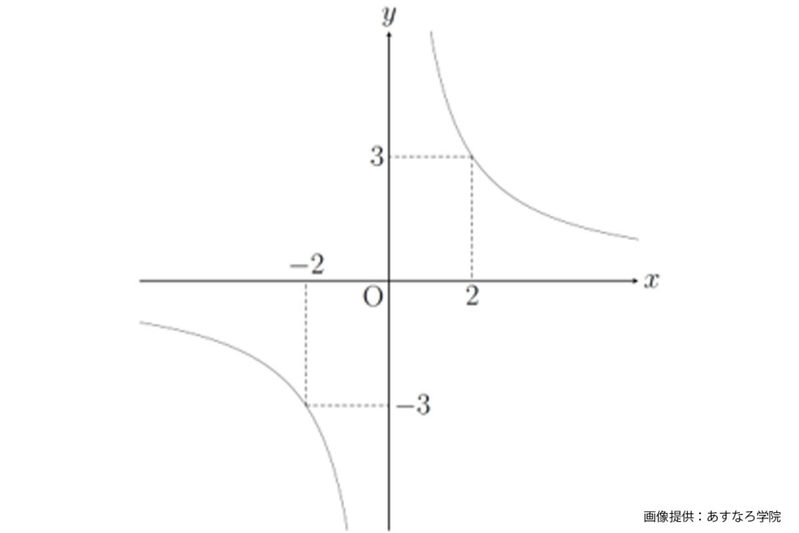
しかし、もしも「●÷0=0」と認識されていた場合、どうなるだろうか。
この場合「y=6÷x」という関係式でxの値が0になると、yの値も「6÷0」で0ということになってしまう。そのため、xの値もyの値も両方とも0になるような点、つまりx軸とy軸の交点で「O」と表している場所を通る必要がある。
しかし実際には反比例のグラフは、記事内の図のように「Oを通らないグラフです」として学習するため、「数字を0で割ったら0である」と信じていた場合、矛盾が生じてしまう。
弊害はこれだけでなく、森山氏は「高校数学では『aを実数としてxの方程式 ax=1を解け』といった問題が参考書に載っています。この問題は、単に両辺をaで割って『x=1/a』としてしまう誤答が多いのです」と、さらなる例を挙げる。
続けて、「この解法が誤っているのは『両辺をaで割るという操作は、そもそもaに当てはまる数が0の場合は不可能なのに、そのことを注意せずに両辺をaで割っていること』が理由となります」と説明。
つまり、こちらも生徒が「数字を0で割ることができる」と認識していた場合は破綻してしまい、正しい学習が阻害されるケースが十分に考えられるのだ。



































