光や電子という、世界の根源的な存在に目を向けたとき、それは粒子と波動という一見矛盾した2つの性質を同時に成り立たせていることがわかってきました。
しかし、古典物理学ではその振る舞いを説明することができません。
放射線や線スペクトルの問題から、物理学者たちは原子の内部がどんな構造になっているかに興味の対象を広げていきました。
しかし、原子の内部構造を考え始めると、原子核やその周りに存在する電子の振る舞いは、やはり古典物理学では成立させることができませんでした。
ニュートン以来、世界を支配する盤石な学問だった物理学は、ここで大きな壁にぶつかったのです。
物理学者たちはもはや、使い慣れた古典物理学には別れを告げ、新しい事実に対応した新理論を作るしかなかったのです。
しかしこうして生まれた量子力学には、さまざまな奇妙な性質がありました。
「物事は確率でしかわからない」「観測するまで物事の状態は確定しない」という不可思議な理屈や、「シュレーディンガーの猫」と呼ばれる哀れな猫の思考実験、そしてアインシュタインの「神はサイコロを振らない」という言葉。
そんな誰もが聞き慣れた不思議な量子力学の議論はすべて、エルヴィン・シュレーディンガーの波動方程式が登場してから、その解釈を巡って始まります。
そして、この問題は、共に量子力学の誕生に貢献してきたアインシュタインとボーアを対立させ、議論を戦わせる原因になるのです。
彼らは量子力学の何を受け入れ、何を拒んだのでしょうか?
目次
2つの量子力学
シュレーディンガー方程式は一体何を計算しているのか?
2つの量子力学
物理学において重要な課題の1つが、実験結果と一致した値が導ける方程式(法則)を見つけ出すことです。
しかし、粒子と波動という相容れない2つの性質を示す光や電子の振る舞いは、古典物理学の常識では説明できず、実験と一致した値を計算することもできませんでした。
そこで、ハイゼンベルグは新しい理論「行列力学」を作り出し、これを計算できるようにしました。
これはざっくり言えば、電子の振る舞いについて、取りうる値を全部書き出して行列計算するというものです。
しかし当時の物理学者たちにとって、行列計算はまったく馴染みのない計算方法でした。
しかも数学が得意だったハイゼンベルクは「別に視覚的なイメージが伴わなくても何の問題もないだろう」と考えていたため、ここまでの解説で多用したような、図に描いて解説できるイメージが何もありませんでした。
今記事を読んでいる読者も行列力学が何なのかほとんど意味がわからないでしょうが、実際当時の物理学者たちもこの理論がどんな現象を取り扱っているのかさっぱりわからなかったのです。
物理学は数学とは異なり、目に見える現実の現象を取り扱った学問です。
そのため、現象をイメージもできず、難解な計算方法を強いる行列力学は、物理学者たちもうんざりだったのです。
そんな中、救世主のごとく登場したのが、現代でも誰もがその名を知るエルヴィン・シュレーディンガーです。

シュレーディンガーは、幅広い分野をカバーできる器用な理論家で、他人の研究を分析してわかりやすく解説する能力に長けていました。
あるときシュレーディンガーはアインシュタインの論文の中で引用されていた、ド・ブロイの学位論文を見て興味をもちます。
ド・ブロイの理論は先に説明したように、電子などの物質も光同様に波として振る舞うと主張したもので、その波は物質波(ド・ブロイ波)と呼ばれていました。
シュレーディンガーはこの理論についても、見事な解説を行います。
しかし、その解説を聞いた物理学者のピーター・デバイは「ド・ブロイの理論には物質波を記述する波動方程式が存在しないからナンセンスだ」と指摘しました。
それはシュレーディンガーから見ても、もっともな意見でした。波動方程式がない波の理論など、物理学では話にならないからです。
そこでシュレーディンガーはド・ブロイの言う物質波を記述する波動方程式について考えてみました。
最初シュレーディンガーは特殊相対性理論と矛盾しない波動方程式を考えていましたが、それは実験結果と一致した答えを導けませんでした。
そこで彼は古典物理学の常識は無視して、物質波の波長と、粒子の運動量を結びつける方程式を創作したのです。
そうして誕生したのが、かの有名なシュレーディンガー方程式です。
この波動方程式を基礎にして、シュレーディンガーは新理論『波動力学』を打ち立てます。
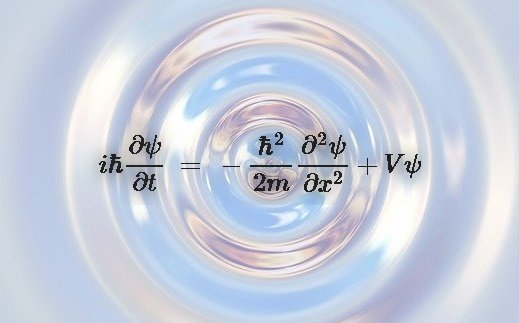
余談ですが、シュレーディンガーはとっかえひっかえ愛人を作るプレイボーイで、この世界に革命を起こす偉大な波動方程式を見つけ出したのも、不倫旅行の最中でした。
そのため、ボルンには「彼のような私生活は私たちのような平凡な人間には理解できない」と言われ、ドイツ人数学者のヘルマン・ヴァイルにはこの偉業を「人生後半のエロスの噴出の賜物だ」、と言われたそうです。
そんなシュレーディンガーの私生活の問題はともかくとして、ハイゼンベルクの行列力学に苦しんでいた物理学者たちは、この波動力学に「待ってました!」とばかりに飛びつきました。
なにせこの理論は謎めいた行列とは異なり、電子の振る舞いを馴染み深い波のイメージで視覚的に説明してくれた上、計算に必要な技術は物理学者たちにとって非常に使い慣れた微分方程式でよかったからです。
これにはプランクもアインシュタインも称賛を贈り、ゾンマーフェルトさえ「行列力学が正しいことは疑う余地がないが、取り扱いが非常に難しく、恐ろしく抽象的だ。シュレーディンガーはそこから我々を救ってくれた」と評しました。
パウリもその明快さに驚愕し感銘を受けたと語り、行列力学の誕生に貢献したボルンさえ波動力学に乗り換えてしまいました。
面白くないのはハイゼンベルクでした。
彼からすれば、突然お株を奪われたようなもので、しかも盟友のパウリにも、師であるボルンにも裏切られたと感じたのです。
ハイゼンベルクは原子レベルの出来事を正しく記述しているのは自分のほうだと考えていました。
しかし、正しいも何も、不思議なことにまったく形式の異なるこの2つの理論は、同じ問題に当てはめた場合、まったく同じ結果を出すのです。
波動方程式を使い波を記述する理論と、行列代数を使い粒子の状態を書き出した理論が、数学的には等価なものだったのです。
この事実はイギリス人の理論物理学者ポール・ディラックによって証明されます。
それは波動と粒子の二重性に、再び直面する問題でした。
シュレーディンガー方程式は一体何を計算しているのか?
物質波を計算する波動方程式を見つけ出し、一世を風靡したシュレーディンガーでしたが、彼自身わかっていない問題がありました。
それはシュレーディンガー方程式が具体的には現実の何の波を計算しているのか? ということでした。
シュレーディンガーの波動方程式は、波動関数ψという波の、ある時刻tにおける、任意の点xの波の形を教えてくれます。
しかしシュレーディンガー自身、この波動関数ψが何を表しているのかわかりませんでした。
波といっているけれど、それは一体何が波打っているんだろう? それはシュレーディンガーを含め、みんなの疑問でした。

水の波は、上下運動する水分子の集団的な動きです。音波も、それは空気中の分子が波打って伝わっているものです。
波はその運動を伝える媒質が存在しなければ成り立ちません。
しかし、シュレーディンガー方程式の計算する物質波は、電子1つの波という古典物理学的な理解では意味不明なものを計算しています。
シュレーディンガーはこれを「電子の電荷が雲のように広がったものだ」という解釈をしました。
波動方程式が表しているものは、ある時刻tの任意の場所xにおける電荷の密度だ、というのが彼の考えでした。
では、数々の実験結果が示す粒子としての電子はなんなのでしょう?
シュレーディンガーはこれを、物質波のピークになった部分を我々が粒子と捉えているだけだと説明しました。
物質波は空間の至るところへ広がって、さまざまな波長の波が干渉を起こしています。それは束ね合わさって波束を作ります。その波束のピークが我々には粒子に見えるのだというのです。
あろうことかシュレーディンガーは、物質波を成立させるために、粒子なんて本当は存在しないと主張したのです。
しかしこの理屈だと、波のピークはいくつもできるので、1つの電子が2つや3つに分裂して観測されても良いということになってしまいます。
どうして電子は1つのポイントに収束するのでしょう?
さらに、波動関数には、水素のような電子1つの場合はいいけれど、ヘリウムのように電子2つを含んだ原子の場合、3次元空間に2つの波があるという記述にならず、次元を足し合わせて6次元空間に存在する1つの波として記述してしまうという性質がありました。
これは電子が原子内に1つ増えるたびに、計算する次元が3つ増えるという恐ろしい状態を作り、ウランの波動関数に至っては276次元空間の波という記述になるのです。
これは物質波がシュレーディンガーの期待したような明快な実在の波ではなく、非常に抽象的な多次元空間の波であることを示していました。
それにシュレーディンガーの説明では、結局粒子性の証拠であるプランクの放射法則も光電効果もコンプトン効果も説明できないのです。
そのため、ボルンにも「シュレーディンガーの偉業は結局数学なのであって、彼の物理学はかなりお粗末だ」と言われてしまいます。
しかし、シュレーディンガーの波動関数が実在の三次元空間の波でないのだとしたら、この波は一体何を表しているのでしょうか?
マックス・ボルンは、この問題に対して、歴史に名を残す重要な解釈を提唱します。
それは、波動関数の確率解釈と呼ばれるものでした。





































