「スピログラフ」の描く線はなぜ魅力的なのか？数学的美しさの秘密

スピログラフはどうやって多様な幾何学模様をつくるのか？

スピログラフで描かれる曲線は、数学用語で「内トロコイド」と呼ばれます。

トロコイドとは、曲線の上を円が転がるときに、円の内部または外部の定点が描く曲線を指します。

円が転がる時、円周上にある点が描く曲線はサイクロイドと呼ばれ、こちらの方が有名ですが、トロコイドはサイクロイドの定点が円周上にないパターンを指しています。

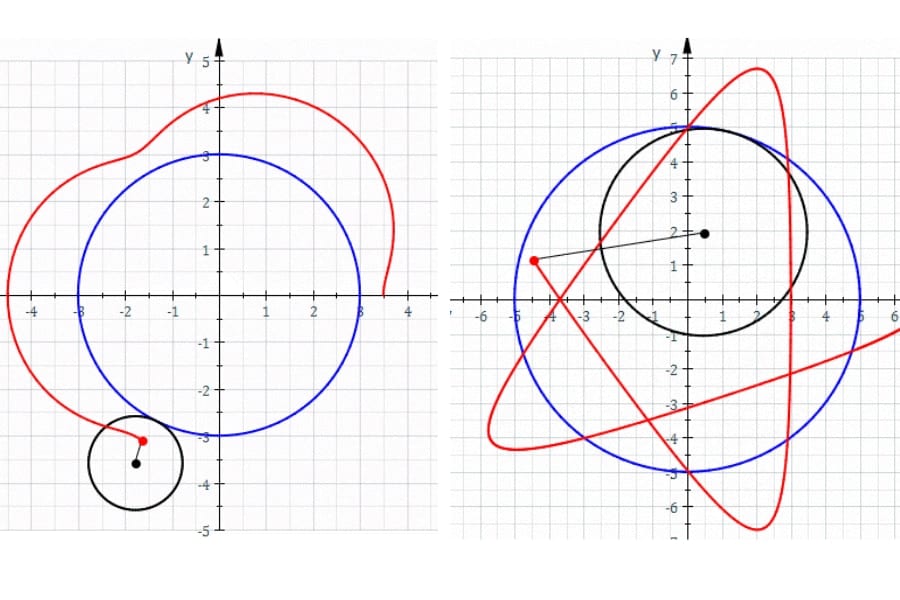
そして特に、円の転がる曲線も円形である場合、その定円の外側を動円が転がったケースを「外トロコイド」、内側を転がったケースを「内トロコイド」と言います。

スピログラフは、大きな歯車状のリングの内側を小さな歯車状の円が転がるので、その内部の穴（定点）に鉛筆を差し込むことで描かれる軌跡は、「内トロコイド」になります。

内トロコイドは次の数式で表現できるため、私たちはスピログラフが描く図形に、一定の法則や緻密さを感じることができます。

別に数式を理解する必要はありませんが、法則性のあるものを私たちは美しいと感じがちです。

複雑で緻密な図形を、単純な玩具で正確に描けることこそが、スピログラフの魅力だと言えるでしょう。

また、1つの要素を変化させるだけでも、完成する図形は大きく異なっていきます。

例えば、同サイズの歯車でも、鉛筆を入れる穴の位置を変化させるだけで、下図のような違いが生まれます。

また内側で転がる歯車のサイズを変化させても、下のように大きな違いが生じます。

そのため、それぞれのパラメータを少しずつ変化させるだけでも、簡単に多種多様な模様を描くことができます。

さらに2つ以上の模様を重ねて描くことで、オリジナルのオシャレな模様をつくることができるでしょう。

上級者たちの中には、専用のマシンを用いてスピログラフのアートを描く人もいるようです。

ここまで来るとさすがに、玩具レベルは超えていますね。

数学的な法則性を持つ図形は、プログラムを使ったり単純な道具の組み合わせることで簡単に描くことができます。しかし、私たちがフリーハンドでそれを再現しようとすると、とてつもなく難しい作業になります。

その作業的なアンバランスさと、秘められた法則性が私たちを魅了してやまない理由でしょう。そしてそれこそが数学の持つ美しさでもあります。

数学理論とアートは深い関係があります。たとえば、多くの人を魅了する画家エッシャーは数学の法則を使ってさまざまな作品を生み出しています。

子供のころ何気なく遊んでいたスピログラフも、大人になってから数学に思いを馳せながら触ると違った印象で見えるかもしれません。

たまには、スピログラフで自分好みの幾何学模様を探してみてはいかがでしょうか。良い気分転換になるかもしれません。