はじめに 「量子力学」を考える上での注意
量子力学が難解な学問という認識は、誰もが抱いているでしょう。
では、なぜ量子力学は難しいのでしょう?
その理由は、量子力学が本来は頭の中でイメージできるような概念を持っていないためです。
とはいえ、量子力学に関するさまざまな図解やたとえ話は、誰でも一度は目にしたことがあると思います。
しかし、実のところ、それらはすべて厳密には正しくないのです。
物理学とは、ニュートンからはじまり、目に見える現象の数々を説明する学問として発展してきました。
ところが、あるときこの理論が崩れ去り、既存の理論では一切説明のつかない事実が次々と発見されたのです。
それはたとえば、光が波として性質と、粒子としての性質どちらでも成立してしまう、というような問題です。
これは頭でイメージしようとしても(あるいは図に描こうとしても)、思い描くことが不可能です。
そのため、物理学者たちはこのイメージできない新しい理論を「量子力学」と呼び、これまでの物理学(古典力学)と切り離しました。
しかし、物理学者も私たちも(数学者を除き)、何が起きているのかイメージできない問題を考えることは非常に不得意で、あまり好きではありません。
そこで、物理学者たちは、馴染み深い古典力学の概念を使って、なんとか量子力学の現象を可視化しようと試みました。
これが私たちのよく知る、量子力学の図説になったのです。
つまり私たちが知っている量子力学に関する説明は、すべて、本来はまったく異なる概念である、古典力学によって無理やり描き出したイメージなのです。
そのため、同じ量子力学の問題でも、解説してる本やサイト、人物によって、全然説明の仕方や解釈が異なってしまう場合もあります。
物理学者たちは、こうした問題をきちんと自覚した上で、うまく利用していますが、私たちはこの事実を理解していないため、頭がこんがらがってしまうのです。
これからはじめる量子力学のお話しも、できる限り視覚的なイメージを交えて解説していきますが、それはあくまで古典力学に置き換えた場合のイメージであって、正しい姿ではないのだということに注意してください。
量子力学はすべて、本来はイメージすることが不可能な問題であることを念頭におきながら見ていけば、多少は量子力学の理不尽な説明にも納得できるかもしれません。
量子の発見

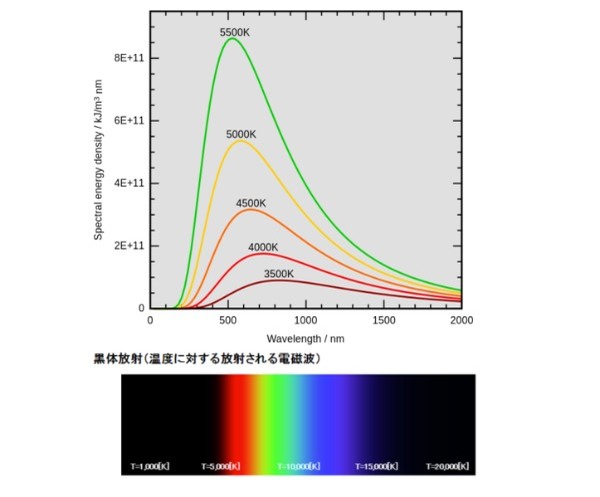
量子力学の歴史はマックス・プランクの行った黒体放射の研究から始まります。
これは光のエネルギーと色の関係を調べる研究でした。
ガスバーナーやコンロの炎は赤色より青色の方が温度が高く、夜空の星々も赤より青く輝く方が高温の星です。
熱した物体は光を放ちますが、これは温度によって色が変わります。これは古くから知られている事実でした。
黒体放射の研究はプランク以前にも多くの研究者が挑戦していましたが、温度と色にどういう関係性が成り立つのか? という問題は長らく謎のままでした。
温度が高いということは、エネルギー量が大きいということを意味しています。
そして光の色は、光の波長によって決まっています。
つまり、光は波長(振動数)でエネルギー量が決まっていると考えることができるのです。
しかし、こうした考えで作られた方程式は、なぜか長波長(赤外領域)に向かうほど実験結果と大きな誤差を生んでしまいました。
なぜ波長が伸びるほど、計算と実験結果はズレてしまうのでしょうか?
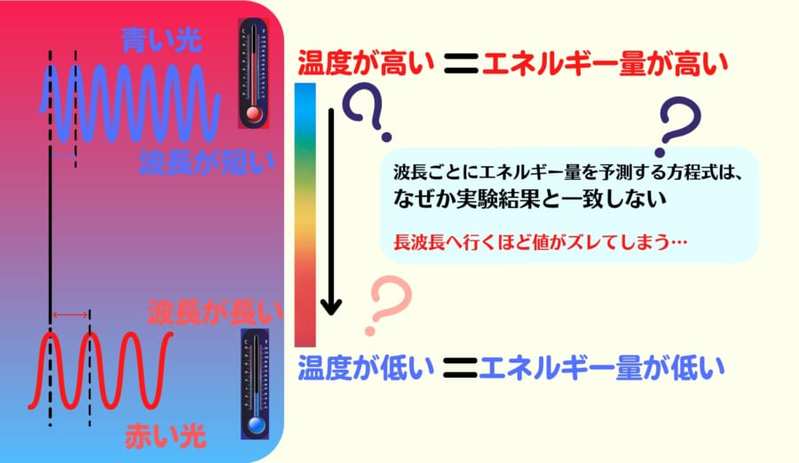
波長が短くなると、振動数は増えることになります。実験結果は振動数が大きいほどエネルギー量も大きくなることを示していました。
そこでプランクは、もっとも単純な解決策として、振動数に定数を掛けるというアイデアを採用します。
光が1回振動するときに現れる最小エネルギー量を実験結果から導き出し、定数として方程式に組み込んだのです。
それが「E = hν」という数式です。
Eとは光のエネルギー、ν(ギリシャ文字「ニュー」)は光の振動数を表します。そしてhとして導入されたのが最小のエネルギー「プランク定数」です。
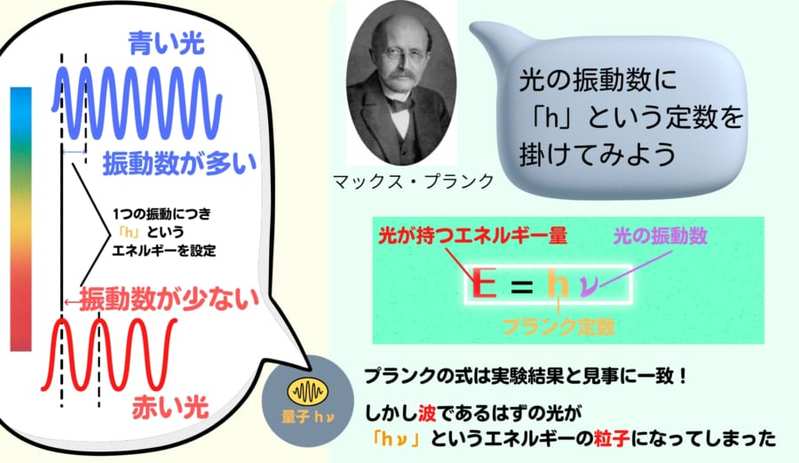
プランク定数hは6.626 × 10-34という恐ろしく小さい値で、日常的なスケールではまず気づくことのできないものです。
そのため、こうした定数が存在することは、プランク以前に誰も気づいていませんでした。
こうして作り出されたプランクの方程式は、実際に検証してみるとピタリと実験結果と一致しました。
しかし、単に定数を掛ければうまく計算できる、なんてことは非常に単純な方法です。
なぜプランク以前の人々は、こんな簡単な方法に気づかなかったのでしょうか?
それは物理学者たちが当たり前の常識として、光を連続して変化する波であると考えていたからです。
プランクのやったように、振動数に定数を掛けてしまうと、光のエネルギーは飛び飛びの値で変化することになってしまいます。
それはすなわち、光が連続した波ではなく、「hν」という飛び飛びの値で変化する粒子として捉えていることになってしまうのです。
そのため、プランクはこれを単に計算の辻褄を合わせるためにやった窮余の策と考えていました。
プランク自身、光の正体が波ではなく、決まったエネルギー素量を持つ粒子だなんて信じることはできなかったのです。
けれど、この「hν」という塊は、後に量子と呼ばれることになり、物理学のさまざまな局面で重要な意味を持つようになるのです。
波? 粒子? 浮上した2重性の問題
光の2重性問題は古くからあり、かのアイザック・ニュートンは光を粒子だと考えていました。
しかし、同時代の物理学者ホイヘンスは、光がエーテルという媒質を伝わる波であると主張しました。
この議論は、最終的に光が波であることが実験によって証明されたため決着します。
それが有名なヤングの二重スリット実験です。
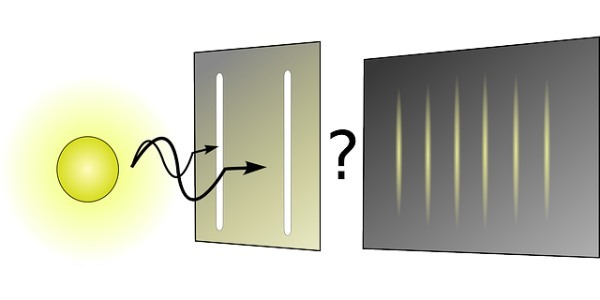
しかし、そんな物理学の常識は、アルベルト・アインシュタインの登場によって打ち砕かれます。
アインシュタインといえば、相対性理論で有名ですが、最初にノーベル賞を受賞した功績は、光電効果の原理を説明した功績によるものでした。
光電効果とは金属にぶつかった光に弾かれて電子が飛び出す現象のことです。
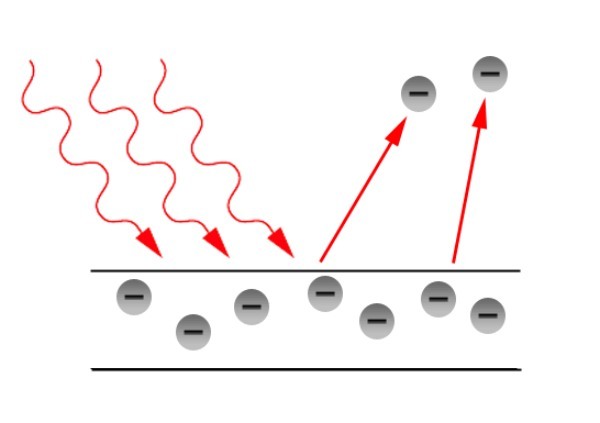
光電効果では、振動数の低い光は長時間照射しても、光量(明るさ)をどんなにあげても、電子が飛び出しません。
ところが照射する光量がどんなに弱くても、振動数の高い光を当てると電子が飛び出しました。
そして、飛び出す電子の運動量は振動数に比例していて、飛び出す電子の数は光量に比例していたのです。
これは光を波として捉えた場合、うまく説明することができませんでした。
アインシュタインは光が振動数に応じたエネルギーを持つ光量子だと仮定すれば、全てがうまく説明できることに気づきました。
この場合、明るくすることは光量子の数を増やすだけということになります。
「電子を追い出すために必要なエネルギーは金属ごとに異なり、飛び出す電子の運動エネルギーは閾値となる光量子の振動数から始まる直線になるはずだ。そして、そのとき描かれるグラフの傾きはプランク定数hになるだろう」
それがアインシュタインの考えでした。
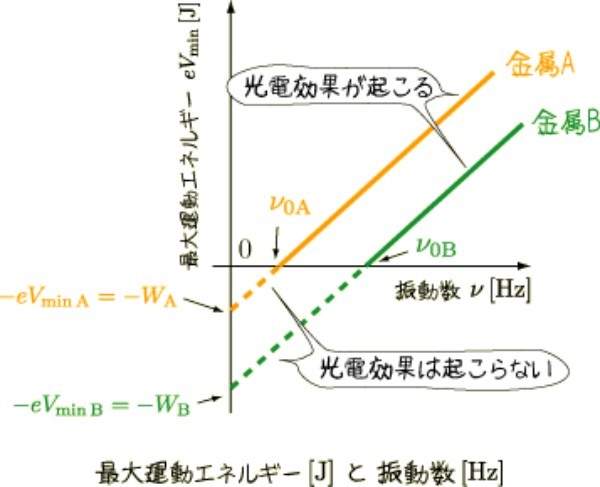
ここでアインシュタインは、光電効果を説明するために、プランクが生み出した量子仮説を利用します。
それは見事に現象を説明していました。
しかし発表当時、光を粒子と捉えるこの理論に多くの物理学者は懐疑的でした。
プランク自身さえ、アインシュタインの光量子に関する論文は素直に受け入れることはできなかったといいます。
アインシュタインは、現代においては偉大な物理学者ですが、当時はスイスの特許局に務める公務員で、仕事の傍ら論文投稿を行うアマチュア科学者でした。
彼の論文は高く評価されましたが、この時点では彼の主張を手放しで信用する人はいなかったのです。
ノーベル賞も、光電効果を説明する方程式の発見について評価したもので、光量子という概念の導入についてはスルーしました。
アメリカの実験物理学者ロバート・ミリカンもその1人で、アインシュタインの間違いを証明してやろうと、10年近くもかけて光電効果の詳細な実験を行いました。
しかしその実験で得られた結果は、全てアインシュタインが正しいことを示すものだったのです。
ミリカンは、この功績により思惑とは正反対にアインシュタインの光電効果理論を実験で証明した人として、ノーベル物理学賞を受賞してしまいます。
しかし、その受賞の場でさえも、ミリカンは「光が粒子であるとは考えられない」と語ったそうです。
結局光は波なのか粒子なのか? どちらについても有力な証拠が出てきてしまい、当時の物理学者たちは大いに混乱しました。













































