「今年はお年玉袋を3つ用意したよ。1つには1万円、あとの2つには千円が入れてある。当たったらあげるから、1つ選んでごらん」
「それでいいの?」
「じゃあ残りの2つのうちハズレの袋1つをどかそう」
「アタリは君が選んでいる袋か、残った袋のうちのどっちかだけど、今ならお年玉袋を変更してもいいよ」
もし、子供時代にこんな意地悪な叔父さんがいたら、貴方はどう答えたでしょうか。
最初の直感を信じて変更せずに勝負しますか、それとも残った方に変更しますか?
実はこの場合、最初に選ばなかった方へ変更したほうが当たる確率が高くなります。これは多くの人が混乱する確率の有名な問題で「モンティ・ホール問題」と呼ばれています。
いくら説明されてもどうしても納得できない人も多いというこの問題。一体どういうからくりがあるのでしょうか。
目次
テレビ番組から生まれた数学問題
最初の選択と途中変更では選択している扉の数が違う
テレビ番組から生まれた数学問題

モンティ・ホール問題は1963年からアメリアで放送されていたゲームショー「Let’s Make a Deal」の1コーナーが発端で生まれた有名な確率問題です。
モンティ・ホールはこの番組で30年近く司会を勤めた人物の名で、学者の名前ではありません。
日本で言えばタモリ問題とか呼んでいる感覚でしょうか。
この番組の中で、モンティ・ホールは参加プレイヤーに3つの扉のうち1つを選ばせるというゲームを行いました。
1つが当たりの扉で、その向こうには商品の自動車があります。残りの2つの扉はハズレでヤギがいます。
最初に語った封筒の例題と同じ流れで、モンティ氏はプレイヤーが選ばなかった扉から、ハズレの扉を開き、「選び直してもいいですよ?」と相手を揺さぶるような提案をします。
この場合、プレイヤーはどうするのが最善の選択なのでしょう?
ほとんどの人は、「ここで扉を選び直しても、そのまま選択を保持しても確率は2分の1で変わらないでしょ?」 と考えました。
しかし、アメリカの雑誌コラムで、とある人物がこの場合の正解は「ドアを変更することだ」と掲載したのです。これは、全米を巻き込む騒動となりました。
「そんなわけねーだろ」と、このコラムに反発した人物の中には、プロの数学者も含まれていました。
なぜこのゲームでは、途中で選択を変更するほうが正解確率が上がるのでしょう?
最初の選択と途中変更では選択している扉の数が違う
この問題で見落としてはならない重要な点は、これがモンティ氏の仕掛ける心理作戦ではないということです。
もし、正解を知っているモンティ氏が最初にプレイヤーの選んだ扉によって、ハズレの扉を開いて選択変更を提案するかどうか選べるなら、これはモンティがプレイヤーを揺さぶるための作戦になり、容易に答えの出ない問題になるでしょう。
しかし、このゲームではモンティ氏は必ず最初の選択後、残った扉からハズレを1つ間引きして、プレイヤーに選択変更の機会を提案するルールになっています。
この条件を踏まえた上で考えると、このゲームは次のような状況になります。
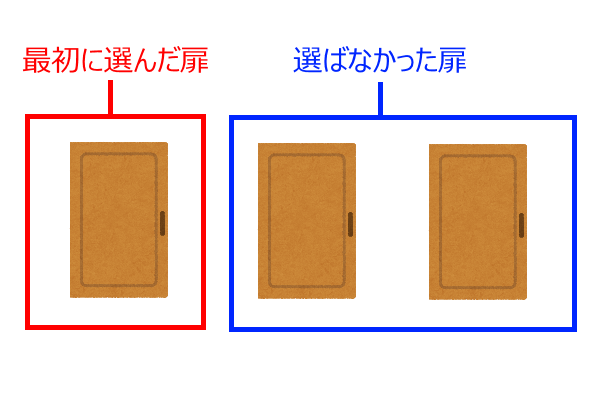
モンティは選ばなかった扉のうちハズレの方を開いてもう一度選び直してもいいと提案します。それはつまり次のような状況です。
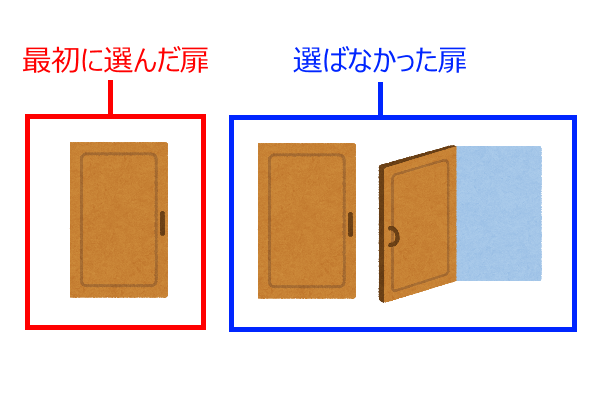
この状況を見るとわかると思いますが、ハズレの扉を明かした上で選択を変更するということは、1度のゲームで2枚の扉を選んでいることに等しいのです。
しかし、多くの人は直感的にこの状況を次のように勘違いして、確率は2分の1だと考えてしまいます。
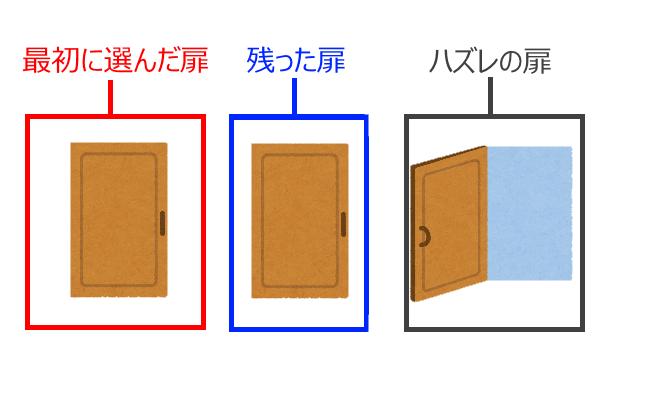
もし最初に扉を選択せずにモンティ氏がハズレの扉を明かしたとしたら、上のイラストのような2択状況になり扉の正解確率は2分の1になります。
しかし、最初に1つ扉を選んでいるというのがミソになります。
どちらでも同じことでしょ? と思ってしまう人はモンティ氏がプレイヤーの選んだ扉を除外してハズレの扉を開いていることに注意しましょう。
それがこの問題のいちばん重要な点です。残された扉は常に2つ1組のセットになっているのです。













































