私たちは現在、太陽や月のサイズと、そこまでの距離を正しく知っています。
しかし、それはNASAとかが言っているから知っているだけであって、自分で調べたわけではありません。
では人類で一番最初に太陽の距離やサイズを知った人たちは、一体どのようにしてその事実を突き止めたのでしょうか?
紀元前の古代ギリシャの哲学者たちは、これを簡単な道具と肉眼、自らの頭脳だけで明らかにしました。
今回はその驚きの方法について解説していきます。
地球の大きさを測定したエラトステネス
古代の人たちは、地球が亀や象の背に乗った平坦な地面だと考えていた…わけではありません。
そんな考えの人もいたかもしれませんが、紀元前のギリシャ人はすでに地球が丸い球であることを理解していました。
このことは月食でできる地球の影が丸いことや、水平線の向こうから船がやって来る時、まずマストの上部が見え、それから徐々に船体が見えてくるという事実から明らかでした。
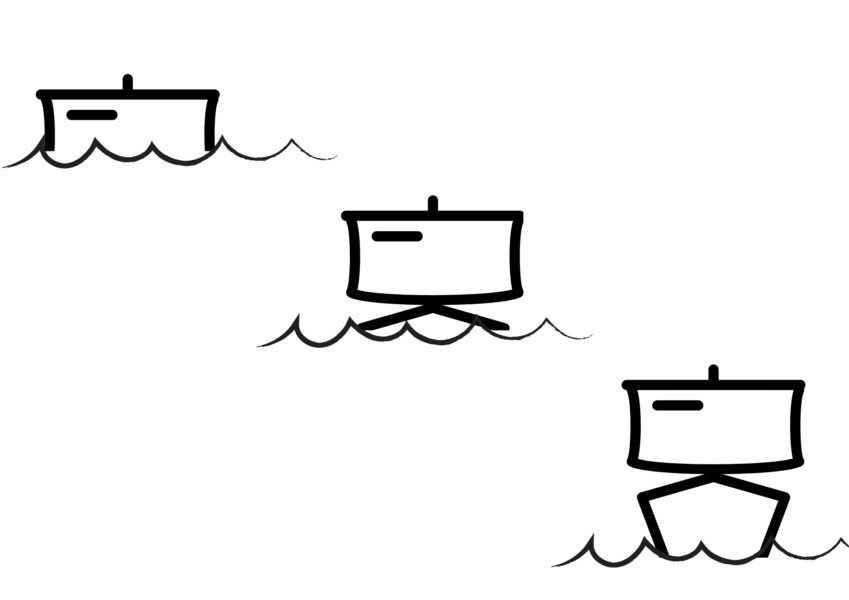
この事実を聞いた子供たちを悩ませる「南半球の人はなぜ落ちないの?」という疑問も、ギリシャ人たちはクリアしていました。
彼らは「すべてのものは宇宙の中心に向かって引かれており、地球は宇宙の中心にある」と考えていたのです。
では地球が球だとして、それは一体どのくらいの大きさなのでしょう?
このことを最初に明らかにしたのが、当時の世界最高学府だったアレクサンドリア図書館の館長エラトステネスでした。

あるときエラトステネスは、エジプト南部シエネの街に「夏至の日の正午になると、底まで明るく太陽で照らされる井戸がある」という話しを耳にします。
彼はこの話から、夏至の正午に太陽はちょうどシエネの井戸の真上に来るのだと考えました。
しかし、シエネから数百km離れたアレクサンドリアでは、決してそんなことは起こりません。
シエネとアレクサンドリアで、同時に太陽が真上に来ないのは地球が球形をしているためだと気づいたエラトステネスは、これを利用して地球の大きさを測ることができないかと考えたのです。
そこで彼は夏至の正午に、アレクサンドリアに棒を立てその影の長さから、アレクサンドリアに差す太陽光の角度を測定しました。
この太陽光の角度は、シエネとアレクサンドリアから地球中心にまっすぐ線を引いたときの角度と同じになります。
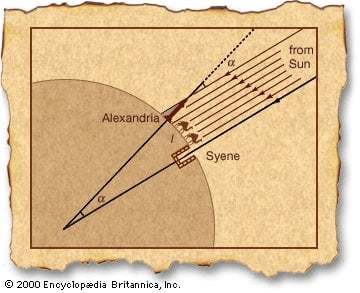
上の図で見ると分かるように、この事実の重要な点は、
【シエネとアレクサンドリアの距離:地球一周の距離 = アレクサンドリアの太陽光の角度:360度】
という関係で一致することです。
つまり、夏至の正午にアレクサンドリアで測った太陽の角度を360度で割れば、シエネからアレクサンドリアまでの距離が地球一周の何%にあたるかを計算することができるのです。
エラトステネシスはこの方法によって、地球を一周した距離が25万スタディオンだと導きました。
スタディオンという単位が、正確にどの程度の距離を表すものだったのかは残念ながら現代には伝わっていません。
しかし、オリンピュアの徒競走で使われる標準的な距離だったという情報から、当時の競技場のサイズを参考に推測すると、エラトステネスの導いた地球の距離は、実際の値から大きくとも15%しかずれていなかった可能性があります。
いずれにせよ重要なのは、たった1本の棒と優れた人間の頭脳によって、紀元前の人々は地球という惑星のおおよそのサイズを知っていたということです。
そして、地球のサイズが分かったことで、彼らは月や太陽についても、その大きさや距離を計算できるようになるのです。
月を測るのは月食と爪
月の大きさを推測する方法は、エラトステネスより以前にアリスタルコスという古代ギリシャの哲学者が考えついていました。
このときアリスタルコスが利用したのが、月が地球の影に隠れてしまう現象「月食」でした。
太陽は月と地球の距離よりもずっと離れたところにあるはずです。そのため月にかかる地球の影は、地球とほぼ同じ大きさだと推測することができます。
月食の時、月が地球の影の真ん中を通っていると仮定すると、月の端が地球の影にかかり始めてから、完全に隠れて消えるまでの時間は月の直径の目安になります。これは50分でした。
そして月が地球の影に入ってから、端が影の外に出てくるまでにかかる時間は地球の直径の目安になります。こちらは200分でした。
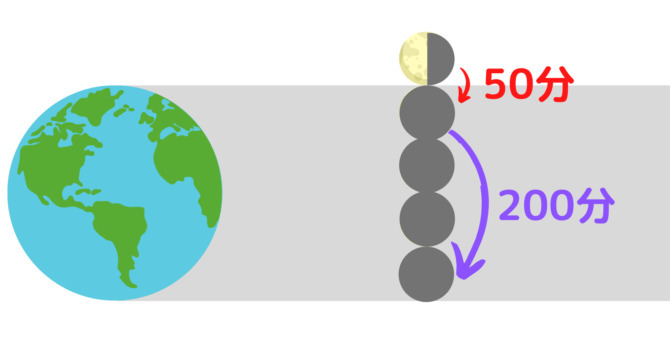
月が完全に隠れるまでに50分、そして地球の影から抜け出すまでに200分かかったということは、月の大きさは地球の約4分の1だと推測することができるのです。
ただアリスタルコスは、この事実に気づいても地球のサイズがわからなかったため、月の大きさを計算することができませんでした。
しかし、エラトステネスは地球一周が25万スタディオンということを発見したので月のサイズも計算することができたのです。
いつまでも謎のスタディオンではわかりにくいので、現代の単位4万キロメートルに直して考えていきましょう。
地球の直径は、外周の「4万キロメートル」をπで割ればいいので「1万2700キロメートル」です。月の直径はその4分の1なので「3200キロメートル」となります。
月の大きさはわかりましたが、果たして月と地球の距離はどうやって求めればいいのでしょうか? これは月の大きささえ分かれば簡単に求めることができます。
満月の夜に、月に向かって腕を伸ばし、人差し指を立てると指先の爪がすっぽりと月を隠してしまいます。このとき指先の爪と、月の大きさはほぼ同じに見えることになります。
これは、爪の大きさと腕の長さの比が、月の大きさと月までの距離の比に等しくなっていると考えることができるのです。
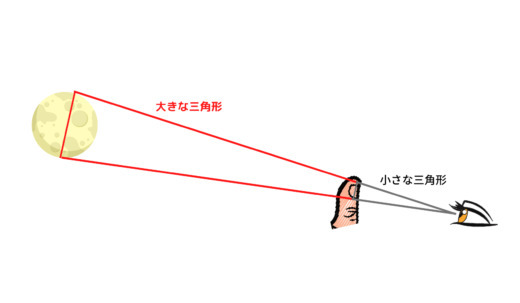
実際はもう少しきちんとした道具を使用して測ったでしょうが、エラトステネスがこうした方法で比率を計算したところ、月までの距離は月の大きさのだいたい120倍だろうと検討がつけられました。
つまり月の直径の120倍、約38万4千キロメートルが地球から月までの距離だとわかったのです。
では、月よりもはるかに遠く、はるかに巨大な太陽を古代ギリシャ人はいかにして測定したのでしょうか?
月を利用した太陽の測定
宇宙の神秘に近づくために、まず人類に必要だったことは、太陽や月が神の化身ではなく、宇宙に浮かぶ天体であると理解することでした。
このことを最初に主張したのは、紀元前400年代の哲学者アナクサゴラスです。

アナクサゴラスは、太陽を神などではなく白く熱い岩石であると主張しました。夜空の星も同様の熱い岩石だが、こちらは非常に遠くにあるので太陽のようには感じられないのだと言ったのです。
さらに月は冷たい岩石であり、太陽の光を反射しているだけだと論じました。
彼の住んでいたアテナイは、かなり学問に寛容な都市でしたが、さすがに太陽や月を神ではなく岩石だ、と主張したことには反発が多く、残念なことに彼は街を離れることになってしまいます。
そんなアナクサゴラスの考えを後に発展させたのが、さきほど月の大きさの測り方でも登場したアリスタルコスです。

アリスタルコスはアナクサゴラスの考える通り、月が太陽光を反射しているなら、半月のとき月と太陽と地球は直角三角形を描いているはずだと考えました。
もしそうなら、地球と太陽の作る角度がわかれば、三角法によって月と地球の距離と地球と太陽の距離の比を明らかにすることができます。
アリスタルコスが実際に半月のとき、太陽と地球が作る角度を測定したところ、それは87°でした。このことからアリスタルコスは、太陽までの距離は、月までの距離のおよそ20倍だと導きました。
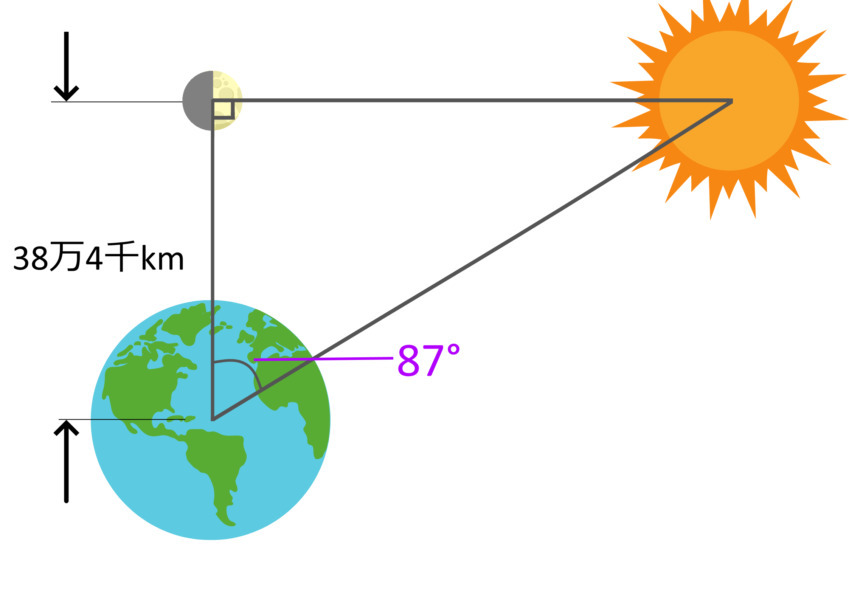
実際は、現代の技術で調べると、この角度は正確には89.85°であることがわかっており、太陽までの距離は月までの距離のおよそ400倍です。
アリスタルコスは、この角度を調べるためにかなりの苦労をしたでしょうが、技術的な精度の限界で正しい値を知ることはできませんでした。
しかし考え方は間違っておらず、ズレがあるものの彼は地球と太陽の距離を推定することができたのです。
では、最後に太陽の大きさはどれほどなのでしょう?
この測定方法はすでに解説しています。
日食のとき、月は太陽をすっぽりと覆い隠してしまいます。このことからアリスタルコスは、地球から見た月と太陽の大きさがほぼ同じであることを知っていました。
だとすれば、さきほど爪と月を使って比を取った方法を、今度は月と太陽で行えばいいのです。
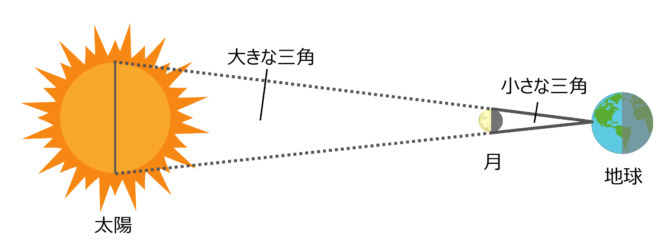
月の大きさと、月までの距離、太陽までの距離はわかっているのですから、
【太陽の大きさ:月の大きさ = 太陽までの距離:月までの距離】
という関係を利用して、おおよその太陽までの距離を知ることができるのです。
こうして、紀元前の昔、古代ギリシャの人々はおおよその太陽までの距離やその大きさまでを計算して知っていました。
現代はさまざまなテクノロジーの進歩によって、複雑な問題を高い精度で調べることができ、私たちは世界中のさまざまな発見を素早く知ることができます。
しかし、1本の棒と優れた頭脳と鋭い観察眼だけで、はるか2000年以上の昔、人類はこれだけの事実を明らかにしていたのです。
こんな話を聞くと、現代の私たちは本当に自分の頭脳を最大限に活かしきれているのかな、と考えさせられてしまいます。
参考文献
『宇宙創成 (新潮文庫)』
提供元・ナゾロジー
【関連記事】
・ウミウシに「セルフ斬首と胴体再生」の新行動を発見 生首から心臓まで再生できる(日本)
・人間に必要な「1日の水分量」は、他の霊長類の半分だと判明! 森からの脱出に成功した要因か
・深海の微生物は「自然に起こる水分解」からエネルギーを得ていた?! エイリアン発見につながる研究結果
・「生体工学網膜」が失明治療に革命を起こす?
・人工培養脳を「乳児の脳」まで生育することに成功













































