約3700年前の古代バビロニアの粘土板に、世界最古とされる幾何学の実用例が発見されました。
この粘土板は、19世紀後半に現在のイラク中部で見つかり、それ以来、イスタンブールの博物館に保管されていたものです。
研究をおこなったニューサウスウェールズ大学(UNSW・豪)の数学者、ダニエル・マンスフィールド氏によると、粘土板に記載されていたのは、のちに「ピタゴラスの定理」として知られる三角関数の原始的な形とのこと。
ピタゴラスより1000年以上も早く、数学史的に非常に重要なものと考えられます。
研究は、8月4日付けで学術誌『Foundations of Science』に掲載されました。
土地区分のための「原始的な三角法」と判明
この粘土板は「Si.427」と呼ばれており、実際に作られたのは、古代バビロニア時代(紀元前1900年〜1600年頃)です。
発見時には、描かれている図形が何を意味するのか分からず、そのまま100年以上も放置されていました。
しかし、マンスフィールド氏は今回の研究で、粘土板の幾何学が「古代バビロニア時代の地籍文書の実例である」ことを明らかにしています。
「地籍文書とは、測量士が土地の境界を定めるために使う図面のことです。
今回のケースでは、土地の一部が売却されて分割された畑について、法的・地理的な詳細が記されています。
ここでは、直角三角形の辺を計算するためのモデル、いわゆるピタゴラスの定理が使用されています。今回の発見は、数学の歴史を語る上で重要な意味を持っているでしょう」と氏は話しています。

一方で、この三角関数は、紀元前2世紀に夜空の星を見て考案された実際の「ピタゴラスの定理」とは大きく違います。
ピタゴラスの定理は、「a2 + b2 = c2」という方程式に当てはまるものです。
直角三角形の直角に隣接する二辺をaとbとし、最も長い斜辺をcとしたとき、a2とb2を足すとc2の値に一致します。
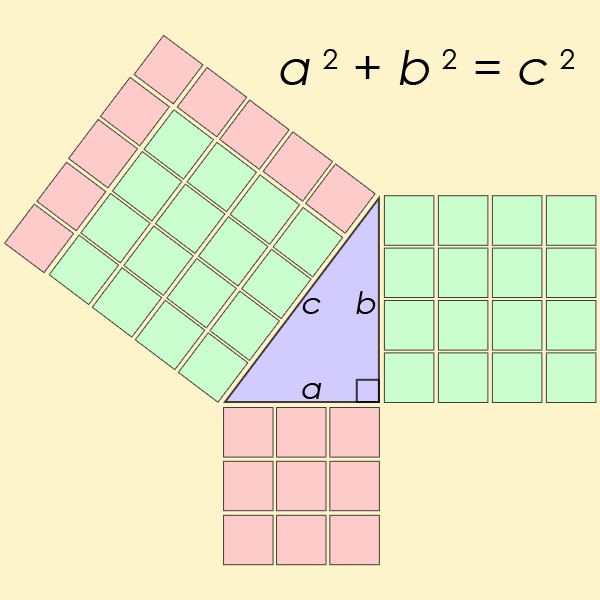
これを使うと、完全な直角を持つ三角形や長方形を描くことができますが、古代バビロニアでは、扱える数字がずっと小さいものでした。
バビロニアは60進法を採用しており、基底の60まで数えると次の位の数1に変えていました。
たとえば、「1秒が60回で1分」や「1分が60回で1時間」などは、60進法の数え方です。
マンスフィールド氏によると「60進法では、5以上の素数を扱うことが難しいため、この三角関数で使える数字も自ずと小さくなる」と指摘します。
そのため、バビロニアの測量士が使ったのは、現代のサイン(sin)、コサイン(cos)、タンジェント(tan)を含む三角法とは異なる、原始的な三角法だったようです。

そして、この原始的な三角法は、土地の境界線の決定に使われたと考えられます。
マンスフィールド氏は、以下のように述べています。
「粘土板は、ちょうど土地が私有化され始めた時代のもので、古代バビロニアの人々は、良好な隣人関係を築くため、明確な境界線を必要としました。
この粘土板が示しているのはまさにそれで、畑を分割した後の新たな境界線の敷設に使用されたのでしょう。
同時代の他のタブレットを見ると、なぜ境界線が必要だったかが分かります。
一つの例として、2つの土地の境にあるナツメヤシの木をめぐる争いで、地元の行政官が測量士を派遣して解決することになったという記録が残されています。
それを踏まえると、土地を正確に測る能力が重要だったことは容易に想像がつくでしょう。」


原始的とはいえ、これは幾何学に対する高度な理解を示すものです。
古代ギリシャの三角法ほど高度ではなかったでしょうが、バビロニア人の数学力は、現在知られているよりずっと進んでいたのかもしれません。
参考文献
This 3,700-Year-Old Tablet Shows The Oldest Known Example of Applied Geometry
Incredible 3700-Year-Old Babylonian Clay Tablet Is World’s Oldest Example of Applied Geometry
元論文
Plimpton 322: A Study of Rectangles
提供元・ナゾロジー
【関連記事】
・ウミウシに「セルフ斬首と胴体再生」の新行動を発見 生首から心臓まで再生できる(日本)
・人間に必要な「1日の水分量」は、他の霊長類の半分だと判明! 森からの脱出に成功した要因か
・深海の微生物は「自然に起こる水分解」からエネルギーを得ていた?! エイリアン発見につながる研究結果
・「生体工学網膜」が失明治療に革命を起こす?
・人工培養脳を「乳児の脳」まで生育することに成功





































