一般相対性理論では、重力によって時空そのものが曲げられると考えられます。
ピンと張ったシーツに重いボウリング玉を置いてシーツがたわむ、あのアナロジーですね。
こうした曲がりの影響で、「過去」と「未来」を単純に分けられない状況も出てきます。
すると、そもそも「時間の矢」や「エントロピーが増える」という概念をどう定義すべきなのか、ややこしい問題が生じるのです。
ここで役立つのが、フラクチュエーション定理という理論です。
これは「ごく稀に起こる逆戻り現象も含めて、全体としてエントロピーがどのくらい増大するか」を統計的に導き出す考え方で、量子レベルの小さな系にも適用可能です。
日常感覚では「混ざったコーヒーとミルクが自然に分離する」ようなことは起こりえないと思いがちですが、微小な世界では確率が極端に低いだけでゼロとは言い切れません。
フラクチュエーション定理は、そうした「極めて小さいけれど逆向きに進む」可能性も含めて、不可逆性を正確に評価できる理論的ルールなのです。
ただ、これまでの議論は主に「重力がほとんど効いていない」平坦な時空を想定していました。
アインシュタインが「重力と熱」を結びつけようと試みた歴史は古いものの、量子レベルで徹底的に論じるのは容易ではありません。
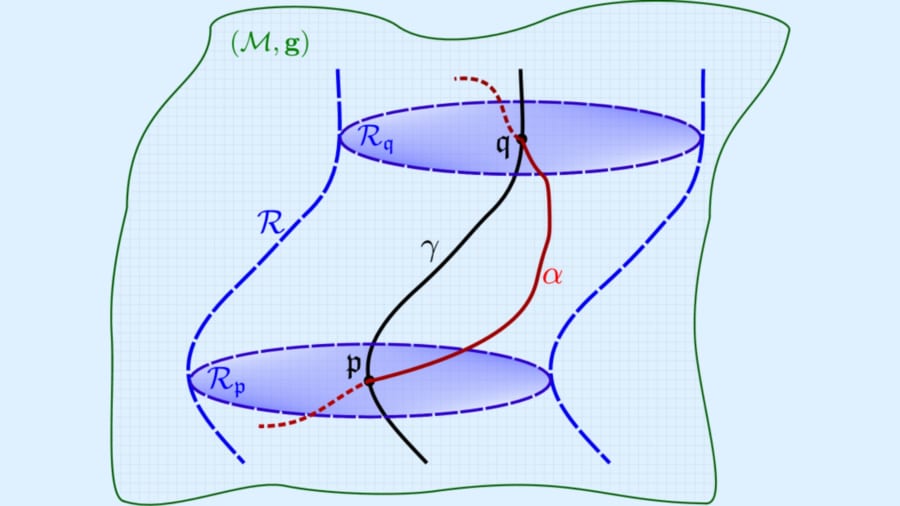
そこで今回の研究グループは、Fermi正規座標という手法で、曲がった時空を細かく“実験室”に区切りながら、量子の世界でエントロピーがどう増えていくかを二点測定方式(TPM)で計算できる枠組みを構築しました。
結果として、観測者がどこに立って(どの世界線に沿って)観測するかによって、エントロピー増加の度合いが理論的に異なる可能性が示されたのです。
重力が曲げるのは空間だけじゃない?量子エントロピーへの挑戦