「3.14」のような「. 」で1より小さい数を区切って表す小数点の表記法は、現在ではごく当たり前のことです。
しかし実はこの表記法の起源は完全には明らかになっておらず、小数点をいつから人類が使い始めたかは曖昧なままです。
そんな中、カナダのトリニティ・ウェスタン大学(TWU)の数学史家により、これまでで最も古い小数点「. 」の表記例が発見されました。
これまで見つかった記録では、ドイツの数学者クリストファー・クラヴィウスが1593年に使用したものが最古でたが、今回はそれより150年も古い、イタリアの数学者で天文学者のジョバンニ・ビアンチーニが1440年代に使ったものが見つかったのです。
研究の詳細は2024年2月17日付で学術誌『Historia Mathematica』に掲載されています。
小数の概念は紀元前から存在した
小数は、整数1よりも小さい数を表すところから生まれた概念です。
人類と小数との出会いはとても古く、古代バビロニア人によって発見されていましたが、当時はまだ「小数点」の概念はありませんでした。
現代の小数と同じ「十進法」における小数の表記は、古代中国で発明されています。
十進法とは、現代で最も日常的に使われている数の表記システムで、0〜9までの10個の数字を使って、どんな数でも表すことができます。
古代中国では紀元前から十進法による小数が使用されていたようです。
例えば、263年に書かれた数学書『九章算術』の中に「八寸六分六釐二秒五忽」という表記がありますが、これを現在のアラビア数字に直すと「8.66025」になります。

このように小数の表記自体は非常に古くからありましたが、ヨーロッパではエジプト式分数表記が普及していたため、小数の導入が遅れました。
分数表記とは、いわゆる「1/2(2分の1)」や「2/5(5分の2)」というような表記の仕方です。
これは現在でも普通に使われていますが、小数と違って、より細かな数字が表記できなかったり、数の大きさを直感的に把握するのが難しいというデメリットがあります。
例えば、8分の85といわれてもピンと来ませんが、10.625と小数に直せば、数の大きさも一発で分かりますし、足し引きなどの計算も簡単になります。
こうした流れの中で、フランドル(現ベルギー)の数学者であるシモン・ステヴィン(1548〜1620)がヨーロッパで初めて小数表記の導入を提唱しました。
ただ彼が考案した小数は「. 」のような小数点を使うものではなく、小数点以下の桁を⓪、①、②、③というような丸囲み数字で表現し間に挿入するものでした。
例えば、1.234を表そうとすると「1⓪2①3②4③」となります。

これは皆さんもおそらく実感したように、非常に読みづらくて分かりにくく、浸透しませんでした。
その後、現代にも使われる小数点「. 」が最初に登場するのは、ドイツの数学者クリストファー・クラヴィウスによる1593年の使用例とされています。
クラヴィウスの天文学論文『Astrolabium』の中に「45.5」というような現代式の小数点の使用例が確認できるのです。
この表記法は小数のイメージを一目でつかむのに非常に有用で、計算にも便利でした。
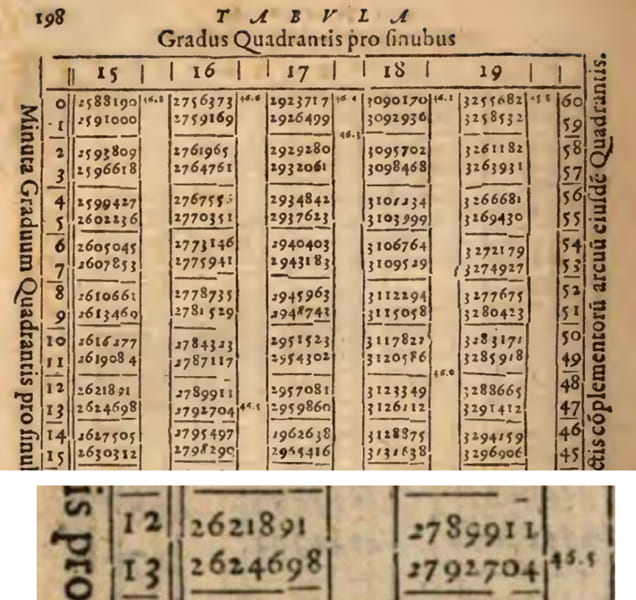
これゆえにクラヴィウスは数学史に偉大な功績を残した人物と考えられていました。
ところが今回の新たな研究で、小数点「. 」はクラヴィウスより150年も前の人物によってすでに使用されていたことが明らかになったのです。
その年代はヨーロッパで初めて小数表記を導入したといわれていたステヴィンよりも前のことでした。










































