高次元構造の結晶? 準結晶とはなんなのか
準結晶は1984年に発見された全く新しい形態の固体のことです。
通常の個体は、結晶かアモルファス(非結晶)でできています。
結晶というのは、規則的なパターンで周期的に原子が格子状に結合したものを指し、多くの固体はこの結晶です。
アモルファスは(非結晶)はそうした規則的なパターンや周期性のない結びつきをした固体のことで、ガラスはアモルファスの1種とされています。
ガラスは固体でもなく、液体でもない特殊な状態の物質だという話を聞いたことのある人も多いでしょうが、それはガラスがアモルファスであるためです。
しかし、準結晶はこの結晶ともアモルファスとも異なります。
では準結晶のなにがそんなに特殊なのかというと、その結晶構造には規則性はあるものの、周期性がないのです。
その意味するところはすぐには理解しづらいので、少し例をあげて説明していきましょう。
下の図は、準結晶の特殊な構造を示す例の1つで、ペンローズ・タイルパターンと呼ばれるものです。
この図は緑と青の2種類のひし形が組み合わされて作られていて、星型のような模様が所々に見えますが、周期性というものを見つけることはできません。
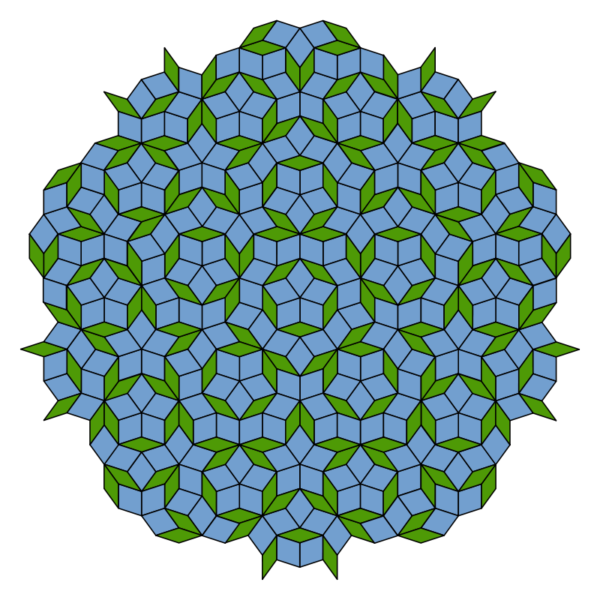
その原因は、この図形が5角形を基本として作られているためです。
あるパターンが周期的に繰り返されるためには、並んだパターンが空間を隙間なく埋める必要があります。
このためには、基本となる図形は、3角形、4角形、6角形をつなげていく必要があります。これらの図形を並べた場合、平面は隙間なく埋めることができます。
しかし、5角形ではそれができません。必ずどこかに隙間ができてしまうのです。
下の図は上のペンローズ・タイルパターンの中心に5角形の補助線をいれたものです。これを見ると、このパターンは補助線の位置でズレてしまっているのがわかると思います。
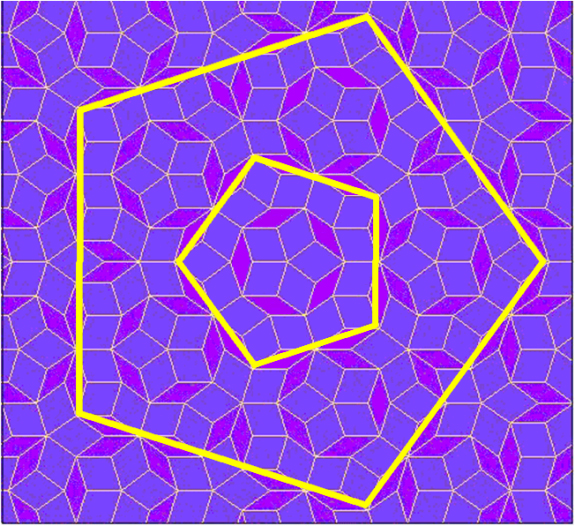
ここで何が言いたいのかというと、5角形で作られた結晶構造というのは理論上ありえないということです。
ところが準結晶は調べると5回の回転対称性が見られるのです。
これはつまり理論上作り出せるはずがない、ペンローズ・タイルパターンの3次元バージョンで準結晶ができていることを意味しています。
あまりに奇妙なため、準結晶を初めて報告したダニエル・シュヒトマンの論文は、初投稿では論文誌への掲載が認められなかったほどです。
しかし、準結晶は現在は確かに存在するということが認められていて、シュヒトマン氏は2011年に「準結晶の発見」という功績によってノーベル化学賞を受賞しています。
では、理論上ありえない立体構造を、どうして準結晶は作り上げることができるのでしょうか?
準結晶は現在もいろいろと研究されていますが、現在の理解の仕方はこれが非常に複雑な多面体が輻輳して空間を綺麗に埋めているからだとされています。
この3次元的な入れ子構造が、本来3次元空間では実現の難しいパターンを実現しているというのです。
そうはいっても多くの学者から否定されていたように、これは3次元的には形成が困難な信じられないくらい複雑な構造です。その複雑さから、準結晶の存在は、世界に私たちが認識できていない余剰次元の構造がある証拠なんじゃないかと考える物理学者もいます。
ただ少なくとも正二十面体準結晶は、三次元空間において、ほとんどの結晶よりも優れた長距離の秩序を持っており、自然に形成される結晶構造の1つであることは確かです。
いずれにせよ準結晶は天然にはまず見られない、非常に特殊な物質です。
そして、今回の研究に戻ります。
今回報告されている赤いトリニタイトから発見された物質は、天然の結晶にはありえない5回の回転対称を持っていました。
つまりこれは人類が作り出した最初の準結晶だったのです。そして、その特殊な組成には、起源の瞬間を示すタイムスタンプが刻まれていたというのです。










































