量子コンピュータは時間を巻き戻したわけじゃなかったので反省して解説してみる

(画像=Credit:maxpixel,『ナゾロジー』より引用)

■「量子コンピュータで時間が巻き戻る」としたニュースが発表され、当サイトでも紹介
■実際は量子コンピュータ内部のシミュレーションを逆向きにしたもので、熱力学や物理法則を破ったわけではない

先日ナゾロジーでも紹介した、「量子コンピュータで時間が巻き戻る」という衝撃的なニュース。ニューズウィークや英国のインディペンデントなど名だたるサイトが、「時間が巻き戻り、バック・トゥ・ザ・フューチャーがかなったようだ」などと報道しました。

しかしこのような記述は元となった論文には記されておらず、ある種の伝言ゲームの果てに発生してしまった誇大広告というオチだったようです…。

本記事ではこの論文に関する誤解を解くため、「時間の矢」とよばれるものについて、誤解を恐れずに簡単に説明していきます。

時間の矢

そもそも時間の矢とはどういうものなのでしょうか？

通常は赤い水と青い水が混ざった紫色の水を、元通りに分離することは起こりません。

これは一見すると当たり前のようですが、物理学の基本法則から考えると実は奇妙なことなのです。物理学の基本法則、例えば振り子の運動で出てくるようなニュートンの運動方程式を考えてみてください。

重要なのは、ある物理現象が起こるならば、「その運動の様子を映像的に逆再生したもの」もまた物理現象としてあり得るということです。

もちろん色の付いた水の混合は振り子の振動とは性質の違う現象なので、常識的には元通りにはなりません。これはなぜかというと、単純に言えばこの2つは現象に関わる粒子の数が違うからです。この違いが、時間反転解を実際の物理現象として実現し得るのかという点に大きな影響を与えるのです。

ここでエントロピーという概念が登場します。乱雑さとも訳されるこの尺度は、粒子の散らばり具合を表しています。そして、1個1個の粒子の状態の組み合わせの総数の内、「色のついた水が混じり合っている状態」は「分離していると言える状態」よりも圧倒的に多いことが分かっています。

(画像=左側のように色で位置が分かれる配位のパターンは少ないが、”混ざっている”と言える配位のパターンは膨大な数に及ぶため、ランダムに動いてもまず色が分離された状態は見られない / Credit: Nazology,『ナゾロジー』より引用)

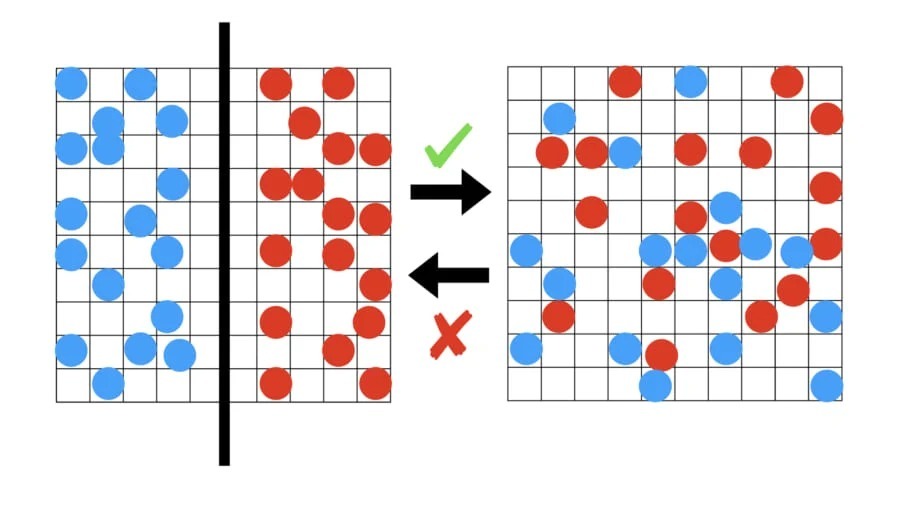
時間が進むにつれて、いずれか1つの組み合わせの状態からもう1つの状態へランダムに移り変わります。混じり合っている状態からまた別の混じり合った状態になることは起こっても、混ぜたものが元の分離された状態に戻る現象は確率的に起こり得ません。

一方、単純な振り子を考えるとき、この場合だと粒子数が1つしかないため、1個の粒子がとる状態の総数は絵の具の問題より圧倒的に少なく、時間反転解も確率的に十分実現しうるのです。

このように「時間の矢」とよばれる時間反転の非対称性は、ある現象が確率的に起こり得るか否かを粒子数と結びつけて考えることができます。