ただ重いというだけで発生する重力。
この力はいったい何なのでしょうか?
最初に万有引力の法則によってこの力を定式化したニュートンは、重力がなぜ生じるか説明することはできませんでした。
その後、20世紀になってアインシュタインが重力とは時空の歪みであるという一般相対性理論を発表します。
現在は重力波を使って遠い宇宙の観測も行っています。
しかし、それでも重力という力は謎だらけで、物理学者たちは未だこの力の解釈について悩み続けています。
重力の不思議について、改めて考えてみましょう。
目次
本当にすべての物体が引き合っているの?
なんで重いものと軽いものが同じ速度で落ちるの? 変じゃない?
本当にすべての物体が引き合っているの?

りんごが木から落ちるのを見るまでもなく、地球上のあらゆる物体は地面に向かって引っ張られています。
それはずっと古代から人々の疑問でした。
アリストテレスは「万物には本来あるべき場所へ戻ろうとする力が働くのだ」と考えました。
彼は鳥が巣へ戻るのも、地面から持ち上げた物が地面に戻っていくのも、同じ原理によるものだと考えたのです。
しかし、太陽や月をはじめとする天体は、空を移動し続けていてあるべき場所があるようには見えません。
物体を地面に引き寄せる力とはなんなのか? それはずっと長い間人類にとっての謎だったのです。
この問題に大きな転機を与えたのが、17世紀の偉大なる科学者アイザック・ニュートンです。
ニュートンは物体に働く「力」というものを明確に定義することで、物体とそこに働く力によって現象を記述する物理学の道を拓きました。
そうなると当然、地面に物質が落ちるという現象についても、力を用いて説明しなければなりません。
そこでニュートンは地球に向かって働く重力というものについて考えます。
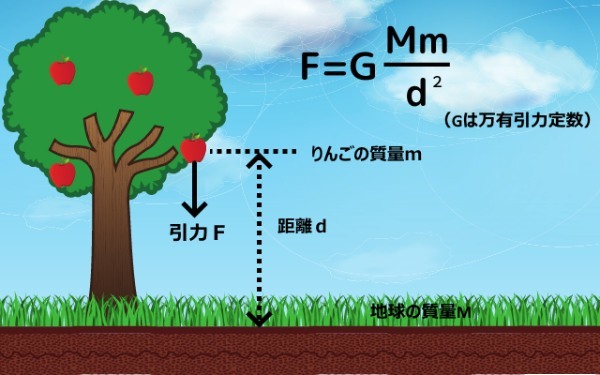
そのとき彼は、これまで誰も考えなかったある重要な事実についてひらめくのです。
「この重力という力は、万有のものだ」
つまり引っ張っているのは地球だけでなく、地球に落ちるりんごなどの物体も同時に地球を引っ張っているのです。
それは地球と月、太陽と地球も互いに引っ張り合っているということです。この考え方によってニュートンは地球に物が落ちる理由と、天空を惑星が運行する理由を1つの理論で説明したのです。
ニュートンはすべての物体に重力があり、質量の大きい物体ほど巨大な重力を生み出すことを明らかにしました。
しかし、それは本当なんでしょうか? そこら辺の石ころも本当にお互い引き合っているんでしょうか?
万有引力の法則を初めて聞いたとき、そんな疑問を抱いた人は多いと思います。
この事実は実験で確認することが非常に困難で、ニュートンが理論を発表してから100年以上も待たなければなりませんでした。
これを証明したのは、イギリスの科学者ヘンリー・キャベンディッシュです。
彼はこのために、2つの鉛玉を乗せたねじり天秤という実験装置を使いました。
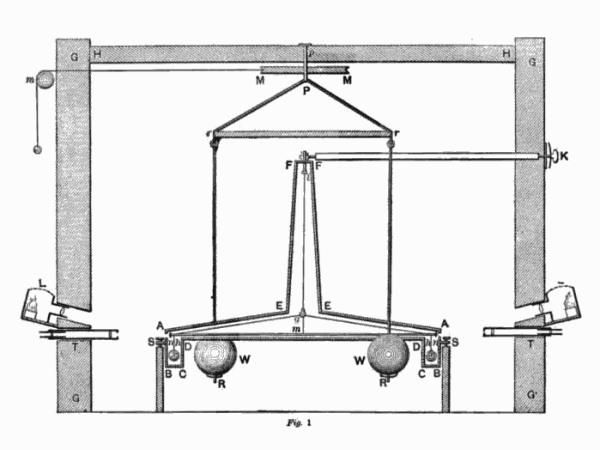
2つの鉛玉を吊るしたワイヤーが、お互いの重力によってねじれるのを、空気や床の振動を受けないようにして確認したのです。
このために彼は実験装置を箱に入れ、さらにそれを小屋の中に置いて、自分ははるか離れた場所から望遠鏡を使って観測したといいます。
重力が万有のものだと確認するのがこれほど困難だった理由は、重力があまりにも弱い力であるためです。
私たちは、普段地球の重力を身体に感じて生活しているので、重力が弱い力だという認識をあまり持てないかもしれません。
しかし、たとえば冷蔵庫にひっつけている小さな磁石は、なぜ重力に引かれて床に落ちないのでしょう?
答えは簡単で、数グラムの磁石が生み出す磁力の方が地球という巨大な物体の生み出す重力より強力だからです。
自然界には、物理学が定める4つの基本的な力(相互作用)、「強い核力」「弱い核力」「電磁力」「重力」がありますが、重力は4つの力の中でも格段に最弱の存在です。
重力があまりにも弱いという問題は、4つの力を統一した理論で語るという物理学の悲願にも障害を生んでいます。
なので、重力という力はこの世界で発生しているのではなく、もっと上の次元から漏れ出てきている力なのではないか、という考え方も登場しています。
重力は後にアインシュタインによって、時空間の歪みなのだと説明されることになりますが、これを2次平面に置き換えて解説しようとすると、2次平面を歪ませるために、3次元空間に働く重力の存在が必要になってしまいます。

こう考えると、たしかに重力が上位の次元から漏れてくる力の一部というのもなんだか納得できる気がしてきます。
「何ゆえに重力はそれほどまで弱いのか?」これは物理学者たちがずっと悩んでいる問いかけなのです。
なんで重いものと軽いものが同じ速度で落ちるの? 変じゃない?
重力の説明を聞いた際、軽いものと重いものの落ちる速度が一緒だと言われて、なんだか釈然としない気分を味わった人はいないでしょうか?
これはガリレオ・ガリレイがピサの斜塔で実験したという逸話が有名です。鉄の玉と木の玉を落としたところ、どちらも同じ速度で落下したと言われています。

羽根がゆっくり落ちるのは空気抵抗があるからで、真空で実験すれば鉄球と同時に落ちる、なんて説明も聞き覚えのある人が多いでしょう。
しかし、なぜそんなことになるのでしょうか?
たとえば、軽い子供なら簡単に抱き上げられますが、お相撲さんを抱き上げるというのはちょっとイメージできません。
それは子供とお相撲さんでは、地球に引っ張られている力が異っているからではないのでしょうか?
重力は重いものほど強く働いているのは明らかです。それなら、なぜ落ちる速度は重さに関係なくなるんでしょう?
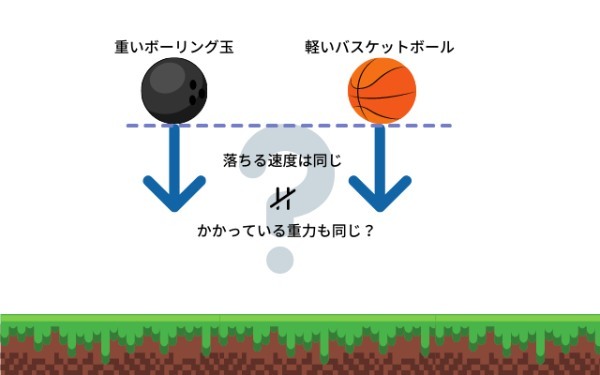
ここでポイントとなるのが「質量」と「重さ」の違いです。
学校でこの2つを習うとき、なぜか区別されていたことを覚えているでしょうか?
実はこの2つは値はピタリと一致しますが、表している性質は異なっています。
「質量」とは物体の「動かしにくさ」を表しています。一方、「重さ」とは物体が「重力に引かれる強さ」を表しています。
たとえば無重力空間の宇宙で、子供とお相撲さんがお互いに押しあったとしましょう。このとき2人はどのように動くでしょうか?
実はこの場合、子供は速く遠くへ飛ばされてしまいますが、お相撲さんはあまり位置を変えない、という結果になります。

それはお相撲さんの方が「質量」が大きい、つまり動かしにくいためです。逆に「質量」が小さい子供は動かしやすいので、簡単に加速がついて移動してしまうわけです。
一方「重さ」は「重力に引かれる強さ」です。重いものは強く重力に引かれます。
部屋の模様替えをするとき、軽い椅子なら簡単に持ち上がりますが、大きなタンスは容易に持ち上げることはできません。
では重いものと、軽いものを一緒に落とすとどうなるでしょう?
当然重いものは強く重力に引かれ、軽いものはあまり重力に引かれません。しかし、動きにくさの点で見ると、重いものは動きにくく、軽いものは簡単に動いてしまいます。
重いものと軽いものが同じ速度で落ちるというのは、この2つの性質がピタリと釣りあっているために起きている現象なのです。
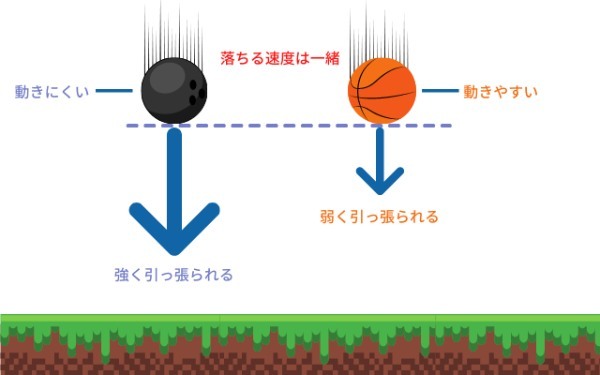
精密な実験でも、「動かしにくさ」と「重力の強さ」という2つの作用は、なぜかぴったりでキャンセルされる関係にあります。
このため、物質はすべて同じ速度で落ちることになるのです。そして「質量」と「重さ」は実質的に同じことになるので、区別して考える必要もなくなってしまうのです。
この2つの効果が一致していてキャンセルされてしまう不思議については、後にアインシュタインが答えを出すことになります。













































