フェルマーの「小定理」をご存知ですか?
「フェルマーの最終定理は聞いたことあるけど、小定理は知らないな」という人が多いかもしれません。
最終定理ほど有名ではない上に、「小定理」という名前ではありますが、見くびってはいけません!
活躍の幅は広く、数学はもちろんのこと暗号理論にまで関わっているスゴイ定理なのです。
今回は、そんな「フェルマーの小定理」について紹介していきます。
フェルマーの小定理とは?

まずは、フェルマーの小定理がどんな定理か見てみましょう。
【フェルマーの小定理】
pを素数とし、整数aとpが互いに素であるとする。このとき、ap-1をpで割った余りは1となる。
(※「素数」とは、1より大きい整数で、1と自分自身以外に正の約数を持たない数のことです。例えば、2や3や5は素数ですが、6は2と3を約数に持つので素数ではありません)
(※「aとpが互いに素」とは、「aとpの最大公約数は1」という意味です。例えば、3と20は互いに素ですが、24と36は、最大公約数が12なので互いに素ではありません)
こう見ると少し難しそうですが、具体例を考えてみるとわかりやすいですよ。
p=5の場合を試してみましょう。
5(pに対応)と互いに素な整数「2,3,4」(aに対応)について、フェルマーの小定理を確認してみます。
それぞれの数を(p-1)乗すれば良いので、今回のケースでは、(5-1)乗、つまり、4乗していきます。
最初に、2を4乗してみると、
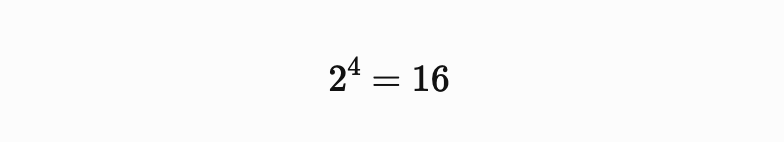
となります。
16は5で割ると1余りますね(商3余り1)。
次に、3を4乗してみると、
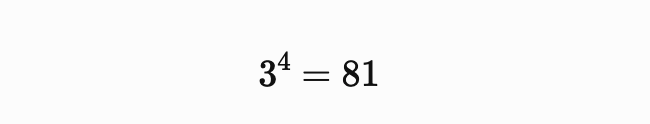
となります。
81も5で割ると1余りますね(商16余り1)。
最後に、4を4乗してみると、
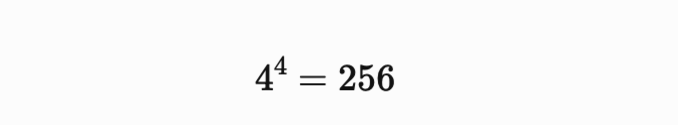
となります。
256も5で割ると1余りますね(商51余り1)。
「5と互いに素な整数」を4乗して、5で割ると、必ず余りが1となるのです!

今度は、p=7の場合を試してみましょう。
7(pに対応)と互いに素な整数「5,6」(aに対応)について、フェルマーの小定理を確認してみます。
それぞれの数を(p-1)乗すれば良いので、今回のケースでは、(7-1)乗、つまり、6乗していきます。
まずは、5を6乗してみると、
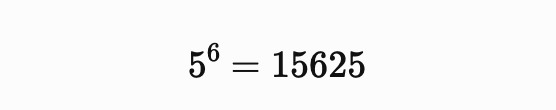
となります。
15625は7で割ると1余ります(商2232余り1)。
次に、6を6乗してみると、

となります。
46656は7で割ると1余ります(商6665余り1)。
7の場合についても、「7と互いに素な整数」を6乗して、7で割ると、必ず余りが1となるのです!
フェルマーの小定理は、5や7だけでなく、「どんな素数pについても、『pと互いに素な整数』を(p-1)乗して、pで割ると、必ず余りが1になる」ということを主張しています。
シンプルながらも、数学の不思議さを感じられる定理ですね。
ぜひ、p=5や7以外についても計算してみてはいかかでしょう。フェルマーの小定理の不思議さを、さらに実感できるはずです!
素数判定に使える!

フェルマーの小定理は素数判定に応用されています。
試しに「221」が素数かどうかを判定してみましょう!
221と互いに素な整数2を、(221-1)乗、つまり、220乗してみます。
計算すると

となりました。
この数を221で割ると、商が7624419306320882294871893406962565235757110979225275022936541360、余り16となります。
もしも、221が素数ならば、フェルマーの小定理を使うと、余りは1にならないとおかしいですよね。このことから、221は素数ではないということがわかります。
このようにフェルマーの小定理を活用した素数判定アルゴリズムは実際に存在しており、「フェルマーテスト」という名前で知られています。
残念ながら、フェルマ―テストは「確率的素数判定」と呼ばれる素数判定であり、その精度は完璧ではありません。
また、今回取りあげた「221の素数判定」は、フェルマーテストのアルゴリズムのほんの一部分を掻い摘んで紹介したものです。興味を持った方は、ぜひフェルマ―テストの全貌を調べてみてくださいね!
フェルマーの小定理は、素数判定アルゴリズムだけでなく、RSA暗号にも使われており、まさに現代になくてはならない定理となっています。「小定理」という名前ではありますが、とても偉大な定理なんですね。
参考文献
高校数学の美しい物語
提供元・ナゾロジー
【関連記事】
・ウミウシに「セルフ斬首と胴体再生」の新行動を発見 生首から心臓まで再生できる(日本)
・人間に必要な「1日の水分量」は、他の霊長類の半分だと判明! 森からの脱出に成功した要因か
・深海の微生物は「自然に起こる水分解」からエネルギーを得ていた?! エイリアン発見につながる研究結果
・「生体工学網膜」が失明治療に革命を起こす?
・人工培養脳を「乳児の脳」まで生育することに成功













































