新型コロナウイルス感染拡大により話題となったワード「指数関数的増加」。数学に馴染みがなくても「ものすごく増えそう」というイメージを抱いた方も多いと思います。
今回は、この指数関数的増加の凄まじさを解説します。
まず、あの豊臣秀吉に仕えたといわれる「曽呂利新左衛門(そろりしんざえもん)の逸話」を紹介し、その後、実際にグラフや数式を見ながら、指数関数的増加を紐解いていきましょう。
果たして、「指数関数的増加」はどれほどまでに凄まじいのでしょうか?
目次
曽呂利新左衛門の逸話
グラフで見る!指数関数的増加の凄まじさ
曽呂利新左衛門の逸話

秀吉に仕えていたといわれる曽呂利新左衛門。非常に頭が良いと評判の人物でした。
この曽呂利新左衛門に関する有名な逸話は「指数関数的増加」のとても良い例になっています。
では、その逸話を見ていきましょう。
ある日、秀吉が「好きな褒美をやろう」と新左衛門に言いました。そこで、新左衛門はこんな褒美を望みます。
「米粒を頂きたいです。1日目は1粒、2日目は倍の2粒、3日目はその倍の4粒といった具合で、次々に倍をしていって、100日目まで米粒を頂きたいです」
秀吉は「なんだ、そんな小さな望みで良いのか」と思って、新左衛門の要求を快諾しました。
こうして、秀吉は新左衛門に毎日米粒を届けることになりました。
1日目は1粒、2日目は2粒、3日目は4粒。15日目に、やっと16384粒となり、茶わん4杯分くらいの米粒になりました
秀吉の家来たちは「新左衛門は、もっとマシな褒美をもらえばよかったのに」と言いながら笑いました。
しかし、20日目には524288粒になり、約10kg分の米粒になりました。23日目には、なんと4194304粒になり、米俵2俵ほどの量に。
驚いた秀吉は、100日目に何粒になるか家来たちに計算させました。すると…
633825300114114700748351602688粒!
兆や京は軽々越えて、「63穣」という、非常に大きな数です。
秀吉は、新左衛門の賢さにしてやられたのでした。
…という逸話です。
新左衛門の要求のポイントは「2を掛け続けること」です。この「掛け算で増えていく」というのが、「指数関数的増加」であり、恐ろしい側面を持っています。
比較のために、
A:1から始めて2を掛けていった場合
B:0から始めて2を足していった場合
として、30日目までの表を作ってみると…
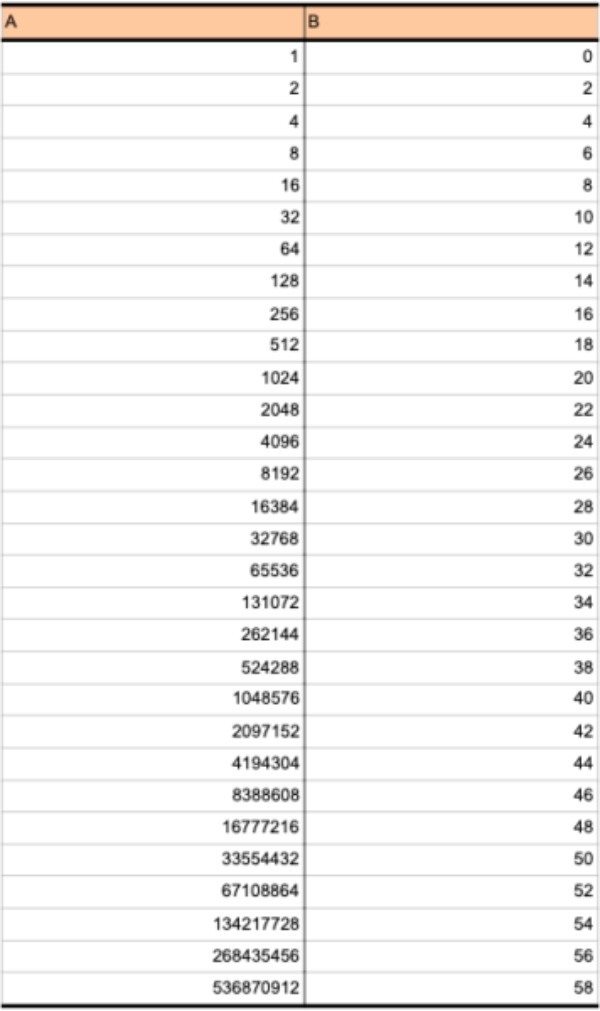
となります。
最初の方はAとBに、大きな差はありません。しかし先に進むと、その差は歴然。Bは一定の速度で増えていくのに対して、Aの増加の速度はどんどん加速していくことがわかります。
30日目まででも536870912粒。これは米俵250俵ほどになります。
秀吉は、最初の「1粒,2粒,4粒」の小ささに、まんまと騙されてしまったようですね…。
グラフで見る!指数関数的増加の凄まじさ
では、この「指数関数的増加」を実際にxy-座標平面上のグラフで見てみましょう。
比較のために、指数関数(先ほどのAのパターンに対応)
と一次関数(先ほどのBのパターンに対応)
の両方のグラフを描いてみます。すると…
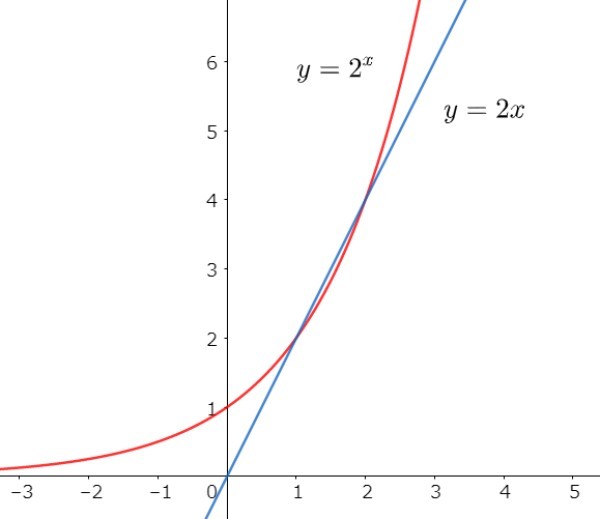
確かに、赤い線の指数関数「2のx乗」の方が、青い線の一次関数「2x」よりも大きくなっていきそうではあります。しかし、その威力はイマイチ見えてきません。
では、縮尺を変えて、もう少し広い視野でグラフを見てみると…
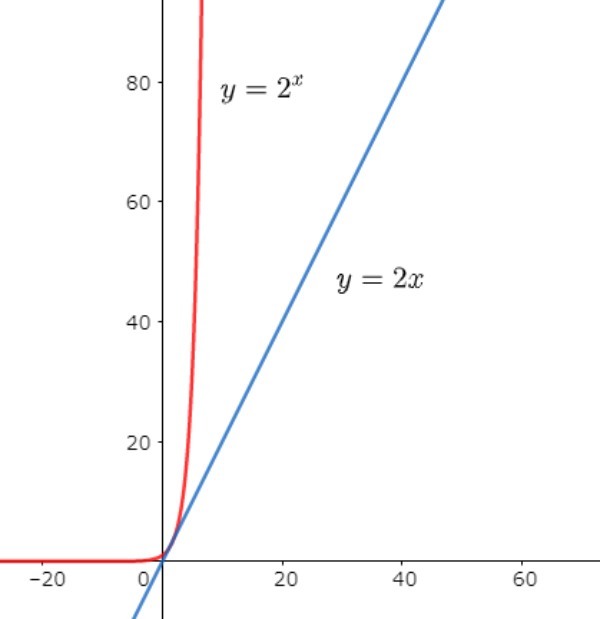
肉眼では「もはや直角じゃないか!?」と思ってしまう程に、指数関数「2のx乗」は一気に増えていることがわかります。直線である一次関数「2x」とは対照的です。
これには、実は「微分」が関わっています。
一次関数「2x」を微分すると、2という定数になります。これは、一次関数「2x」は一定の速度で増えていくことを表しています。
一方、指数関数「2のx乗」を微分すると…
となります。注目してほしいのは、微分しても「2のx乗」が残っている点です。
これは、指数関数「2のx乗」の増加率もまた、指数関数的に増加することを表しています。
つまり、指数関数は猛烈にガンガン加速して増えていくのです。
おまけとして、一次関数「2x」よりも、大きくなりやすい二次関数「xの2乗」を採用して、指数関数「2のx乗」と比べてみます。
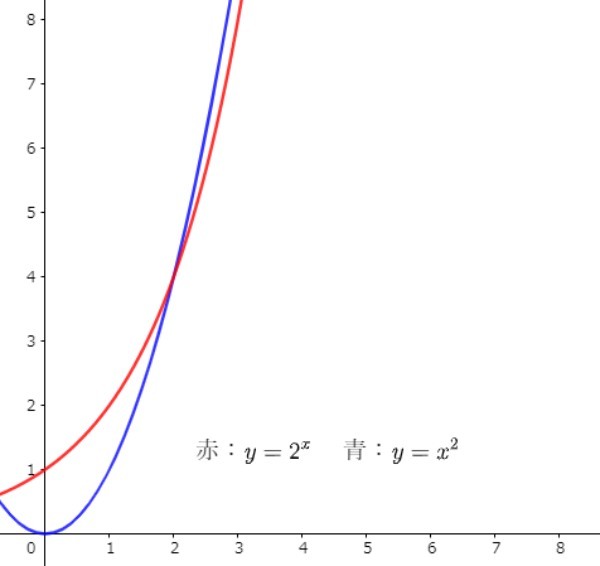
赤い線の指数関数「2のx乗」が、青い線の二次関数「xの2乗」に負けています!
ついに指数関数にも負けが訪れたか…と思いつつ、グラフの縮尺を変えてみると…
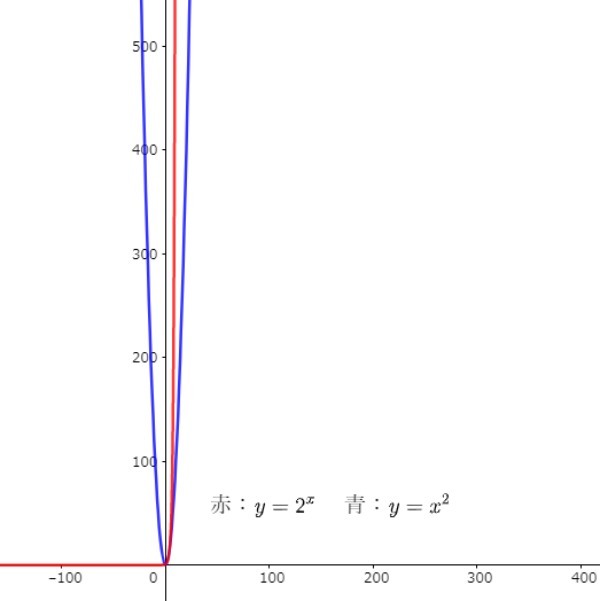
さすが指数関数!二次関数にも、しっかり勝利していたのでした。













































