目次
フーコーの振り子の原理は?
フーコーの振り子の軌道シミュレーション

point
- 地球の自転はフーコーの振り子で証明できる
- フーコーの振り子の原理はコリオリの力
- フーコーの振り子はwebサイト上でシミュレーションできる
科学博物館に行くと、必ずと言っていいほど大きな振り子が展示されていますよね。
この振り子は、フーコーの振り子といいます。
フランスの物理学者であるレオン・フーコーが1851年、パリのパンテオン寺院で、巨大な振り子を用いて地球の自転を証明したことから名づけられました。
フーコーの振り子の原理は?
では、なぜ巨大な振り子が地球の自転を証明できるのでしょうか。実は、この巨大な振り子はまっすぐ直線的に振れることはなく、微妙に軌道がずれながら振れます。
これこそが自転を証明するカギになるのです。
キーワードは、『コリオリの力』。
まずは、イメージをつかみやすいように簡単な例を紹介します。
走っている人が電柱を見ると、電柱は後ろに遠ざかっていきますよね。ところが、第3者の視点で走っている人と電柱を見ると、電柱は静止しています。
実際には静止している電柱が、何の力も受けていないのに動いて見える、という矛盾が生じるのです。
そこで、この矛盾を解消する為に『慣性力』という見かけの力を導入します。「走っている人から見て、進行方向とは逆に慣性力がかかっているので、電柱は遠ざかる。」という説明ができるようになりました。
回転座標系にも同じような現象が起こるのです。
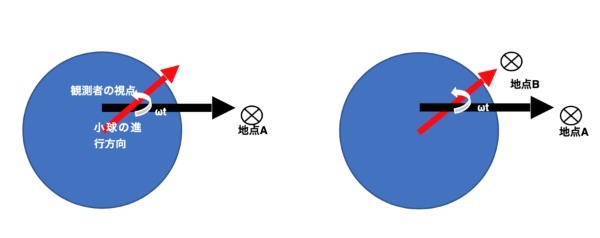
時刻0に、角速度ωで回転する円盤の中心Oから、小球を地点Aに速度vで打ち出すとします。円盤の外部から見ると、まっすぐに打ち出された球は時刻ωtには地点Aにあります。
しかし、観測者の目線の先を地点Bとすると、「目の前に打ち出したはずの球が、目線の先の地点Bではなく、地点Aに遠ざかった」ように見えるのです。
このとき小球にはたらいているように見える力のことを、『コリオリの力』といいます。
これを 数式で表すと、
F(コリオリの力)=2mvω
となります。
振り子の軌道が回転しているように見えるという現象もこのようにして説明できるので、地球自体が回転していることを証明できるのです。
フーコーの振り子の軌道シミュレーション
そんなフーコーの振り子ですが、自分で実験するのは難しいでしょう。巨大なおもり、長い糸、そしてそれを吊るす広い空間が必要ですから。
しかし、誰でも簡単に振り子の軌道を観察できる方法があります。それは、『シミュレーション』です。
サイトにアクセスしてみてください。
『フーコーの振り子』
※白紙のページが表示される場合は、『JAVA』というアプリケーションをダウンロードする必要があります。
サイトにアクセスすると、以下のようなページが表示されます。

ここで、ページの上部に変数を入力していきます。
・地点緯度
振り子の軌道は緯度に依存するので、シミュレーションしたい場所の緯度を調べて入力します。
そこで、『経度は関係ないの?』という疑問が出てきますよね。
結論から言うと、経度は関係ありません。
なぜなら、自転軸に平行な運動にはコリオリの力がはたらかないからです。
難しい数式や定理はここでは割愛しますが、簡単に説明します。
コリオリの力は、回転体において移動方向と垂直な方向に運動している物体の速度に比例します。
つまり、移動方向に対する速度の垂直成分がない経度方向には、コリオリの力がはたらきません。
・振り子の振幅
振り子の回転角は振幅には依存しませんが、値を大きくするほど、回転する軌道の幅が細かくなります。
・描画間隔
値を大きくするほど、データを細かく取ることができますが、大きくしすぎるとデータを取るのに時間がかかってしまいます。
初期値であるms=1でのシミュレーションがおすすめです。
・振り子の長さ
中学校や高校で、振り子の振幅は振り子の長さに依存するということを習ったと思います。
このシミュレーションでも振り子の長さを設定できるので、いろいろな値を入力してシミュレーションしてみると良いでしょう。
・計算回数
『計算回数1回』=『1秒』です。
例えば、実際の振り子が1時間でどのような軌道を描くのかを観察したい場合にはn=3600、1日でどのように動くのかを観察したい場合にはn=86400と入力します。
また、このシミュレーションでは実際の運動がかなり早送りで再生されるので、長時間観察する必要もありません。
入力変数にもよりますが、すべて初期値の状態でシミュレーションすると、1時間の振り子の動きがおよそ15秒程度でわかります。
・図形拡大倍率
図形を拡大表示したい場合に、この変数の値を大きくします。
値を大きくすると全体像が表示されませんので、軌道全体を見たい場合には初期値のままでシミュレーションすることをおすすめします。













































