Point
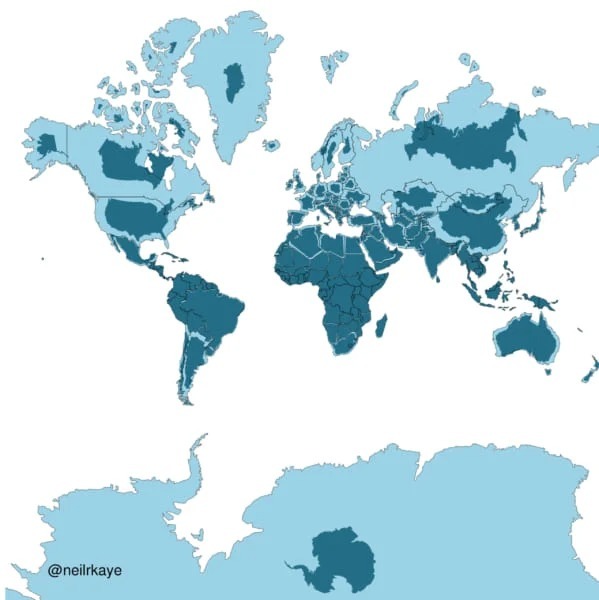
■平面の地図に描かれた陸地と実際の陸地の面積を比較すると、高緯度になるほど大きくズレていく
■これは地球が球体であり、地球上の陸地は曲率を含んだ非ユークリッド幾何学の図形であるためだ
■非ユークリッド幾何学では、平行線が途中で交わってしまうなど、平面図形での常識が通用しない
こんなに違うの?
データサイエンティストのNeil Kaye氏がTwitter上で、実際の陸地サイズと地図上の大きさを比較した画像を掲載。その落差が話題になっています。
色の濃い部分が、該当箇所の実際の面積を表しています。これを見ると、赤道から離れた地域ほど地図上のサイズと実際の面積が乖離していることがわかります。
ここで、最近トランプ大統領が買収を目論んでいると話題のグリーンランドを見てみましょう。
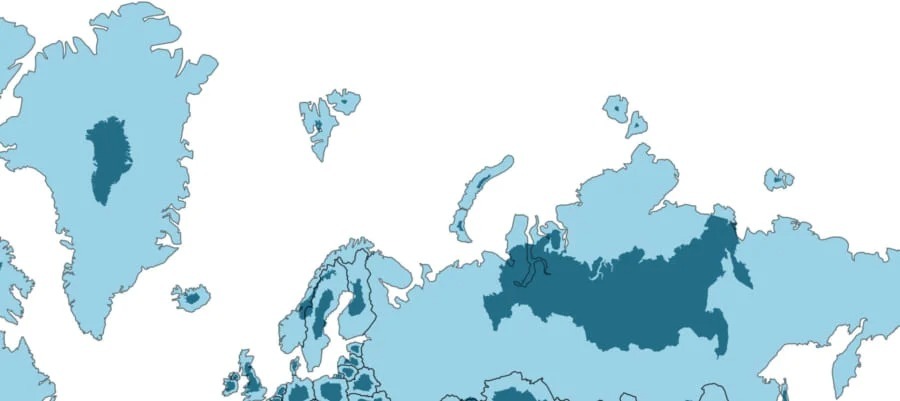
どう見てもデカすぎですね。島なのにアフリカ大陸と同じくらいの大きさをしています。
これは何もデンマークが盛っているわけではありません。売り物じゃないし当然です。ロシアはやりかねないという気もしますが、もちろんそんなことはありません。
こうした地図の問題は、地球が球体であることが原因です。
「そのくらいなら知ってるよ」と思った人も多いかもしれませんが、これには単純なようで意外と複雑な数学の問題が潜んでいます。ここでは、そんな地図が歪む理由について解説していきましょう。
空間が歪んだ図形 非ユークリッド幾何学の世界
学校では、「三角形の内角の和は180°」や「平行線は永遠に交わらない」と教わりますが、こうした図形に関する当たり前のルールは紀元前にエウクレイデスが発見したもので、ユークリッド幾何学と呼ばれています。
ところが、図形を曲面などに描いた場合、こうした当たり前のルールが破綻してしまうのです。これを非ユークリッド幾何学といいます。
地球のような球体の上に図形を描いた場合は、この非ユークリッド幾何学の問題になります。
例えば、赤道と90°で交わる直線を2本描いたとします。これは平面上では平行線になるので交わることはありません。しかし、地球儀などに同じ線を引くと、平行線なのに北極点(または南極点)で線が交わってしまいます。

曲面では平行線はどこかで交わってしまうのです。このため、球面上ではすべての角度が90°というおかしな三角形も作ることができます。この場合、三角形の内角の和は180°を超えて270°になってしまいます。
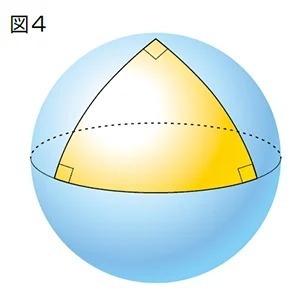
この様に、球面上に描かれた図形は、非ユークリッド幾何学に従うため、平面の図形の常識には従ってくれません。そのため地球上の陸地についても、平面の地図にすべての情報を正確に描き出すことは不可能となるのです。
平面地図に用いられているメルカトル図法は、あらゆる地点で角度を正しく保存しています。これは羅針盤を用いた航海では非常に便利なので、世界に広く普及しました。
しかし、残念なことにこの図法では面積や、地図上の2点間の最短距離は正しく表現することができないのです。









































