「フェルマーの最終定理」この名前は数学に興味があってもなくても一度は耳にしたことのある有名な問題でしょう。
この問題は1995年にイギリス生まれの数学者アンドリュー・ワイルズによって証明され最終的な解決を迎えましたが、その裏には数世紀に渡る、数々の数学者たちのドラマが潜んでいます。
ワイルズ1人の知恵だけでは、この問題を解決することはできなかったでしょう。
ワイルズは直接「フェルマーの最終定理」を証明したわけではなく、この問題とはまるで無関係に見える、ある日本人数学者の「予想」を証明することで、この長年の問題に終止符を打ちました。
難しい数学の証明には興味がないという人も、「フェルマーの最終定理」にまつわる数学ドラマを聞けば、その複雑な証明がどうやって実現したかわかるかもしれません。
ここでは「フェルマーの最終定理」が解かれれるまでのいきさつを、2回に分けて解説していきます。
「フェルマーの最終定理」とはどんな問題か?

「私はこの命題について、真に驚くべき証明を見出したが、それを記すにはここはあまりに余白が足りない」
360年前、フランスの数学者ピエール・ド・フェルマーはたったこれだけのメモを問題の脇に書き残してこの世を去ってしまいました。
フェルマーは今で言うところの承認欲求がまるでない人物でした。
自分で見つけた発見を世の中で認めてもらおうとはまったく考えず、1人で答えを見つけて1人で満足し喜んでいるだけだったのです。
しかし、そんなフェルマーの誰にも教えなかった「真に驚くべき証明」は、「フェルマーの最終定理」として数世紀先の時代まで彼の名を轟かせることになります。
難問とされながらもフェルマーの最終定理が一般にも非常に有名なのは、子供でも理解できる極めて単純な問いかけにあります。
フェルマーは、「xn + yn = zn という式のnが3以上のとき解がない(つまり絶対に式が成立しなくなる)」と言っています。
しかし、この式のnが2の場合、それは誰もが中学校で習う「ピタゴラスの定理(三平方の定理)」になります。
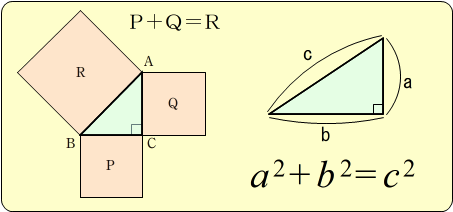
つまり「n=2」であれば、この「xn + yn = zn」という式を成立される「X,Y,Z」の解はたくさん存在するのです。それが「nが3以上」なった途端まったく成立しなくなるというのは、なんだかおかしな気がします。
例えば命題に含まれるように、nを3にして考えてみましょう。この場合、式は2つの異なる立方体の体積の和で新しくもっと大きな立方体が作れるか? という計算をしていることになります。
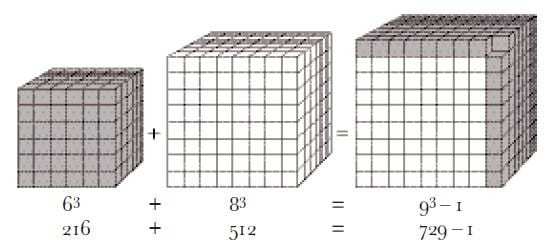
順々に数を当てはめて見ると、上の画像のように「6の3乗」と「8の3乗」を足したとき、「9の3乗より1少ない」という答えが出てきます。
非常におしい答えです。この調子ならすぐに成立する3つのX,Y,Zの組み合わせが見つかりそうな気もします。
ところが、そんな数はいくら探してもまったく見つからないのです。
ピタゴラスの定理に無限の解が存在する証明は、紀元前の数学者エウクレイデスが著書「原論」の中で紹介しています。
同じ式でnが2の場合、無限に解が存在すると証明できるなら、その逆に3以上で解が存在しないと証明することはそんなに難しくないような気がしてしまいます。
最終的にフェルマーの最終定理を証明したアンドリュー・ワイルズは、10歳のときにこの問題を図書館で見つけ、なぜ多くの数学者がこんな問題につまずいているのだろうか? と不思議に思いました。
きっと何か重要な鍵を見落としているだけで、あっさり証明できるんじゃないかと幼少時代のワイルズは思ったのです。
しかし、それは他の多くの数学者たちが落ちた危険な落とし穴でした。以後ワイルズは30年以上、この問題の呪縛に捕らわれることになります。
無限を証明する難しさ

解が無限に存在することを示す証明は、比較的簡単に解決される場合があります。
例えば、数学者エウクレイデスは素数が無限に存在するのか? それとも有限なのか? という議論に対して、無限に存在することを証明しています。
その証明は以下のようなものです。
「素数が有限と仮定して、すべての素数をかけ合わせた数に1を足したとき、それは新しい素数になる。
もし割ることができた場合、その数を割れる未知の素数が存在していることになってしまう。
故に素数は有限ではない」
数行に収まるほどの簡潔な証明です。
しかし、無限に組み合わせの作れる数式に解が一切存在しないということを証明するのは非常に困難です。
特にフェルマーの最終定理では、非常に巨大な乗数の計算にまで言及しています。
この場合「xn + yn = zn」が3乗どころか、100乗でも1万乗でも無限の乗数で計算しても解は存在しないと証明しなくてはなりません。
しかし、1万乗とか1京乗なんてところまで計算していったら、ひょっとして神様の気まぐれで1つくらい成立する数が出てくるかもしれません。
実はフェルマーは4乗の場合に解がないという証明はきちんと書き残していました。
それを利用してレオンハルト・オイラーは3乗の場合に解がないという証明を成功させています。
これらの証明から、さらにnが「3の倍数のとき」と「4の倍数のとき」解が存在しないと証明することができました。
しかし、こんな調子で証明を続けていても埒が明きません。証明するべき「n」は、3以上の無限に連なる数字たちなのです。
この問題を解決するためには、もっと違う視点の考え方が必要だったのです。
数学史の流れを変えた二人の日本人

ここで少しフェルマーの問題から離れ、戦後の日本に話しを移しましょう。
戦後の日本の数学界では、教授陣がすっかり疲れ果て、研究への気力を失っていました。
しかし若手数学者たちは熱意に溢れていて、コミュニティを作って互いに新しいアイデアについて話し合い、勉強していました。
そんな中に、フェルマーの最終定理解決の最重要人物となる二人の若手数学者が登場します。それが谷山豊(たにやま とよ)と志村五郎(しむら ごろう)です。
1955年、日光で数学国際シンポジウムが開かれます。
日本の若手数学者は自分たちの研究を世界に発信するチャンスだと、このシンポジウムの際に、アイデアをまとめたプリントを世界の研究者たちに配って意見を求めました。
その中に、谷山のある重要なアイデアも含まれていました。それが後に数学界に衝撃を与える重要理論「谷山-志村予想」の雛形となるものでした。
「すべての楕円曲線はモジュラーである」
それが谷山の主張した理論の内容です。
非常に簡潔な一文ですが、ほとんどの人には何を言っているのか意味がわからないでしょう。しかし、これは数学者から見ると思いもしなかった画期的なことを言っていたのです。
谷山はまるで映画にでも出てきそうな、ぼんやり型の天才だったと言われていて、靴紐なんていちいち結び直すのは馬鹿らしいからと結ばなかったそうです。
彼はひらめきが先行していたようで、それは数学で何より重要なことでした。
ただあまりに発想が飛躍しすぎていた谷山のアイデアは、このときほとんどの学者たちに「事実とは思えない」と受け入れてはもらえませんでした。
そして、残念なことに谷山はこのシンポジウムの開かれた3年後に自殺してしまいます。自殺の理由は不明です。
谷山の死後、その意志を引き継いだのは志村五郎でした。
志村は図書館で谷山と同じ本を借りようとした縁で知り合い、それ以来数学研究の盟友となっていました。
彼はなんとか、亡き友人のアイデアを形にしようと、その意味を死物狂いで理解し、アイデアを支える理論付けを行っていきます。
そして発表されるのが「谷山-志村予想」です。
数学における「予想」とは、限りなく真であると考えられるが証明はできていない命題につけられる呼び名です。「予想」が証明されるとそれは「定理」になります。
アンドリュー・ワイルズは「フェルマーの最終定理」を証明した人として世間で話題になりましたが、実はフェルマーの最終定理を直接証明したわけではありません。
ワイルズが成し遂げたのは、この「谷山-志村予想」の証明です。
「すべての楕円曲線はモジュラーである」このことを証明することで数世紀の間、世界の数学者の頭を悩ませ続けた「フェルマーの最終定理」の無限の証明が完了してしまったのです。
これは一体どういうことなのでしょうか?
次回はその意味について解説します。
参考文献
フェルマーの最終定理 (新潮文庫)
数学の大統一に挑む(文藝春秋)
提供元・ナゾロジー
【関連記事】
・ウミウシに「セルフ斬首と胴体再生」の新行動を発見 生首から心臓まで再生できる(日本)
・人間に必要な「1日の水分量」は、他の霊長類の半分だと判明! 森からの脱出に成功した要因か
・深海の微生物は「自然に起こる水分解」からエネルギーを得ていた?! エイリアン発見につながる研究結果
・「生体工学網膜」が失明治療に革命を起こす?
・人工培養脳を「乳児の脳」まで生育することに成功













































