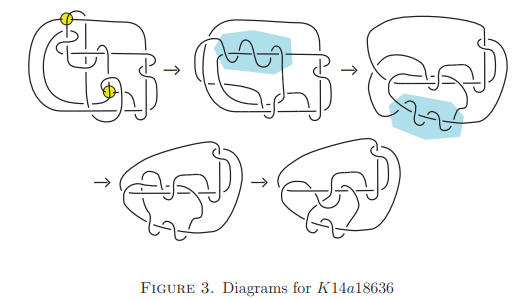
このような結び目の反例が本当に存在するのでしょうか?
謎を解明するために、研究者たちはまず、具体的に調べられるような、分かりやすい結び目を用意して調査を進めました。
最初に研究者たちが注目したのは、「トーラス結び目」と呼ばれる特別な結び目です。
トーラス結び目というのは、ドーナツのような輪の形をしたもの(トーラス)の表面に、規則的なパターンで紐をぐるぐると巻きつけて作った結び目のことです。
このような結び目は、規則正しい形をしているため、数学者にとって非常に分析がしやすく、よく研究の対象にされています。
このトーラス結び目の中でも、特に有名で数学者によく知られている結び目があります。
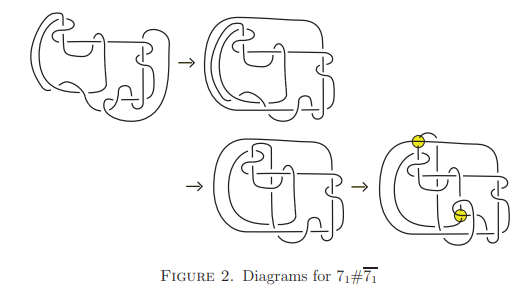
それは、「2回巻き」と「7回巻き」という規則的なパターンでトーラスの表面に巻かれた結び目(「(2,7)-トーラス結び目」と呼ばれるもの)で、数学者たちはこれを「7₁」という記号で表しています。
この「7₁」という結び目は、最低でも「3回」、紐の上下関係を入れ替えるような操作をしないと完全にほどけないことがすでに分かっています。
つまり、「7₁」はそれなりにほどくのが難しい結び目なのです。